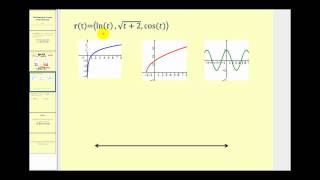
The Domain of a Vector Valued Function
This video explains how to determine the domain of a vector valued function. http://mathispower4u.yolasite.com/
From playlist Vector Valued Function

Introduction to Vector Valued Functions
This video introduces vector valued functions. http://mathispower4u.yolasite.com/
From playlist Vector Valued Function

Probability Density Functions (3 of 7: Unknowns in the function)
More resources available at www.misterwootube.com
From playlist Random Variables

Chp9Pr41: Probability Density Functions
A continuous random variable can be described using a function called the probability density function. This video shows us how to prove that a function is a probability density function. This is Chapter 9 Problem 41 from the MATH1231/1241 algebra notes. Presented by Dr Diana Combe from th
From playlist Mathematics 1B (Algebra)

Probability Distribution Functions
We explore the idea of continuous probability density functions in a classical context, with a ball bouncing around in a box, as a preparation for the study of wavefunctions in quantum mechanics.
From playlist Quantum Mechanics Uploads

Probability Distribution Functions and Cumulative Distribution Functions
In this video we discuss the concept of probability distributions. These commonly take one of two forms, either the probability distribution function, f(x), or the cumulative distribution function, F(x). We examine both discrete and continuous versions of both functions and illustrate th
From playlist Probability

This calculus 2 video tutorial provides a basic introduction into probability density functions. It explains how to find the probability that a continuous random variable such as x in somewhere between two values by evaluating the definite integral from a to b. The probability is equival
From playlist New Calculus Video Playlist

Slava Rychkov - “Bootstrap” method in physics and mathematics
Slava Rychkov (IHES) In the last 10-15 years, “bootstrap” was applied to problems as disparate as critical exponents of second-order phase transitions, scattering of elementary particles, chaotic dynamical systems, and Laplacian spectra on hyperbolic manifolds. This produced many new comp
From playlist Azat Miftakhov Days Against the War

Ex: Function Arithmetic - Determine Function Values from a Table
This video explains how to find the sum, difference, product, and quotient of two functions using the graphs of the two functions. Site: http://mathispower4u.com
From playlist The Properties of Functions

Complex Brunn–Minkowski theory and positivity of vector bundles – Bo Berndtsson – ICM2018
Geometry | Analysis and Operator Algebras Invited Lecture 5.2 | 8.2 Complex Brunn–Minkowski theory and positivity of vector bundles Bo Berndtsson Abstract: This is a survey of results on positivity of vector bundles, inspired by the Brunn–Minkowski and Prékopa theorems. Applications to c
From playlist Geometry

Background material on the Cauchy-Riemann equations (Lecture 1) by Debraj Chakrabarti
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019

Branched Holomorphic Cartan Geometries by Sorin Dumitrescu
DISCUSSION MEETING ANALYTIC AND ALGEBRAIC GEOMETRY DATE:19 March 2018 to 24 March 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore. Complex analytic geometry is a very broad area of mathematics straddling differential geometry, algebraic geometry and analysis. Much of the interactions be
From playlist Analytic and Algebraic Geometry-2018

Steve Zelditch - Critical Points of Random Super-potentials and Spin Glasses
In the early 2000s, one often heard that the vacuum counting problem in string theory was like a spin glass problem. My talk will review results of Douglas, Shiffman, and myself on probabilistic methods for counting vacua of certain string theories. I then review some more recent results b
From playlist Mikefest: A conference in honor of Michael Douglas' 60th birthday

Quantum Yang-Mills theory in two dimensions: exact versus perturbative - Nguyen
Analysis Seminar Topic: Quantum Yang-Mills theory in two dimensions: exact versus perturbative Speaker: Timothy Nguyen Date: Wednesday, April 6 The conventional perturbative approach and the nonperturbative lattice approach are the two standard yet very distinct formulations of quantu
From playlist Mathematics

Petru Constantinescu - On the distribution of modular symbols and cohomology classes
Motivated by a series of conjectures of Mazur, Rubin and Stein, the study of the arithmetic statistics of modular symbols has received a lot of attention in recent years. In this talk, I will highlight several results about the distribution of modular symbols, including their Gaussian dist
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Compatibility of Explicit Reciprocity Laws by Shanwen Wang
Program Recent developments around p-adic modular forms (ONLINE) ORGANIZERS: Debargha Banerjee (IISER Pune, India) and Denis Benois (University of Bordeaux, France) DATE: 30 November 2020 to 04 December 2020 VENUE: Online This is a follow up of the conference organized last year arou
From playlist Recent Developments Around P-adic Modular Forms (Online)

Automorphisms of K3 surfaces – Serge Cantat – ICM2018
Dynamical Systems and Ordinary Differential Equations | Algebraic and Complex Geometry Invited Lecture 9.13 | 4.12 Automorphisms of K3 surfaces Serge Cantat Abstract: Holomorphic diffeomorphisms of K3 surfaces have nice dynamical properties. I will survey the main theorems concerning the
From playlist Algebraic & Complex Geometry

Nigel Higson: The Oka principle and Novodvorskii’s theorem
Talk by Jonathan Rosenberg in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-Seminar.html on November 11, 2020.
From playlist Global Noncommutative Geometry Seminar (Americas)

Probability Density Function of the Normal Distribution
More resources available at www.misterwootube.com
From playlist Random Variables
