
Hubble Dazzling First Light Images in HD
Watch this and other space videos at http://SpaceRip.com Spectacular new images from distant space that you must see to believe. The revolutionary Hubble Space Telescope will continue to open our eyes to the universe.
From playlist Frontiers of Deep Space

The International Space Station continues an uninterrupted human presence in space as a test-bed for future exploration beyond low-Earth orbit and the only science lab in microgravity. This music video featuring the space station and its crews is set to the song "World" by recording artist
From playlist Real Space Stations - YouTube Space Lab with Liam & Brad

Ask the Space Lab Expert: What is Space?
Have you ever wanted to go to Space? In this first episode of Space Lab, Brad and Liam from "World of the Orange" take you on an adventure to discover exactly what is Space. You'll find out about the solar system, the big bang, Sci-Fi movies that are becoming reality, and more!
From playlist What is Space? YouTube Space Lab with Liam and Brad

The Human Body in Space - What happens to your body in space? Start learning with Brilliant today for FREE: http://brilliant.org/aperture Follow me on Instagram: https://www.instagram.com/mcewen/ Space is the final frontier. But you know, it’s not like space has a lot going on. There is q
From playlist Science & Technology 🚀

The Universe is always surprising us with how little we know about... the Universe. It's continuously presenting us with stuff we never imagined, or even thought possible. The search for extrasolar planets is a great example. Since we started, astronomers have turned up over a thousand
From playlist Planets and Moons

What exactly is space? Brian Greene explains what the "stuff" around us is. Subscribe to our YouTube Channel for all the latest from World Science U. Visit our Website: http://www.worldscienceu.com/ Like us on Facebook: https://www.facebook.com/worldscienceu Follow us on Twitter: https:
From playlist Science Unplugged: Physics
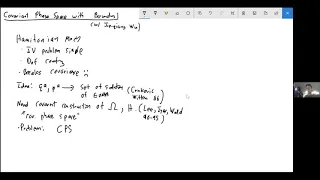
Covariant Phase Space with Boundaries - Daniel Harlow
More videos on http://video.ias.edu
From playlist Natural Sciences

Hidden Dimensions: Exploring Hyperspace
Extra dimensions of space—the idea that we are immersed in hyperspace—may be key to explaining the fundamental nature of the universe. Relativity introduced time as the fourth dimension, and Einstein’s subsequent work envisioned more dimensions still--but ultimately hit a dead end. Modern
From playlist Science

What'll It Take to Find Life? Searching the Universe for Biosignatures
The supertelescopes are coming, enormous ground and space-based observatories that’ll let us directly observe the atmospheres of distant worlds. We know there’s life on Earth, and our atmosphere tells the tale, so can we do the same thing with extrasolar planets? It turns out, coming up wi
From playlist Searching for Earth 2.0

CGSR Seminar Series | War in Space: Strategy, Spacepower, Geopolitics
Speaker Biography Bleddyn Bowen primary research interests concern modern warfare, politics, and security in outer space, as well as classical strategic theory. Dr. Bowen provides research-led teaching in his 3rd year specialist module PL3144 Politics and War in Outer Space. He is the au
From playlist Center for Global Security Research

10. The Four Fundamental Subspaces
MIT 18.06 Linear Algebra, Spring 2005 Instructor: Gilbert Strang View the complete course: http://ocw.mit.edu/18-06S05 YouTube Playlist: https://www.youtube.com/playlist?list=PLE7DDD91010BC51F8 10. The Four Fundamental Subspaces License: Creative Commons BY-NC-SA More information at http
From playlist MIT 18.06 Linear Algebra, Spring 2005
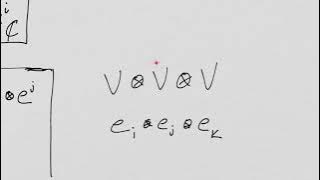
[Lesson 11] QED Prerequisites - Tensor Product Spaces
We take a detour from the Angular Momentum Mind Map to cover the important topic of Tensor Product spaces in the Dirac Formalism. In quantum mechanics, the notion of tensors is hidden under the hood of the formalism and this lesson opens that hood. The goal is to make us confident that we
From playlist QED- Prerequisite Topics

Nicolò Zava (3/17/23): Every stable invariant of finite metric spaces produces false positives
In computational topology and geometry, the Gromov-Hausdorff distance between metric spaces provides a theoretical framework to tackle the problem of shape recognition and comparison. However, the direct computation of the Gromov-Hausdorff distance between finite metric spaces is known to
From playlist Vietoris-Rips Seminar

CGSR Seminar Series | U.S. National Security Space Strategy: The Cold War to the Present
Talk Abstract At the present time, U.S. government officials are faced with the increasingly complex task of protecting critical national security space infrastructure in a rapidly evolving threat environment. When placed in a historical context, we find that anxiety about space security
From playlist Center for Global Security Research

Vice President Pence Calls for Human Missions to Moon, Mars at National Space Council
Vice President Mike Pence called for returning U.S. astronauts to the Moon and eventual missions to Mars during the first meeting of the National Space Council, held on October 5 at the Smithsonian National Air and Space Museum’s Steven F. Udvar-Hazy Center, outside Washington. Chaired by
From playlist Return to the Moon Playlist

Sanjay Mishra: Preservation of Properties during Topological Equivalence of Function Space
Sanjay Mishra, Lovely Professional University Title: Preservation of Properties during Topological Equivalence of Function Space The study of convergence of sequence of functions is the most important and active area of research in theoretical mathematics that solve several problems of app
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

Marvels of Space-Time | Episode 705 | Closer To Truth
Einstein showed that space and time are essentially the same thing-a single entity, space-time. But space and time seem so radically different. How could space and time be literally the same thing? Featuring interviews with Max Tegmark, J. Gott, Juan Maldacena, Fotini Markopoulou, and Joh
From playlist Closer To Truth | Season 7

CS224W: Machine Learning with Graphs | 2021 | Lecture 19.2 - Hyperbolic Graph Embeddings
For more information about Stanford’s Artificial Intelligence professional and graduate programs, visit: https://stanford.io/3Brc7vN Jure Leskovec Computer Science, PhD In previous lectures, we focused on graph representation learning in Euclidean embedding spaces. In this lecture, we in
From playlist Stanford CS224W: Machine Learning with Graphs

Extra-terrestrial Oceans | Your Cosmos | Earth Lab
Could there be life be at the bottom of these extra-terrestrial oceans? We may think of space as being barren and dry, but scientists have discovered that we are not the only blue planet in our solar system. NASA are launching missions to fly drones on distant moons to explore methane o
From playlist Your Cosmos

What is a Tensor 13: Realization of a Vector Space
What is a Tensor 13: Realization of a Vector Space Note: There is an error at 3:26. The equality I write down is only true for orthonormal basis vectors! There will always be a relationship between (e_\mu, e_\nu) and (e^\mu , e^\nu) but it wont always be as simple as I wrote down! For som
From playlist What is a Tensor?