
Proof: a³ - a is always divisible by 6 (2 of 2: Proof by exhaustion)
More resources available at www.misterwootube.com
From playlist The Nature of Proof

Turing Machines and The Halting Problem (Part 2)
The Halting Problem has fascinated thousands of computer scientists from around the world. A major part of Computing Logic, the proof of the halting problem proves that computers can't do everything. Check out the video to learn more about why computers work the way they do! For Turing Ma
From playlist Math

Introduction to Proof by Counter Example
This video provides an introduction to the proof method of proof by counter example. mathispower4u.com
From playlist Symbolic Logic and Proofs (Discrete Math)

What does it mean to be Turing Complete? Is HTML & CSS Turing Complete? #shorts #compsci #programming #math
From playlist CS101

Introduction to Proof by Induction: Prove 1+3+5+…+(2n-1)=n^2
This video introduces proof by induction and proves 1+3+5+…+(2n-1) equals n^2. mathispower4u.com
From playlist Sequences (Discrete Math)

Proofs by contradiction -- Proofs
This lecture is on Introduction to Higher Mathematics (Proofs). For more see http://calculus123.com.
From playlist Proofs

How to Prove a Function is Injective(one-to-one) Using the Definition
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys How to prove a function is injective. Injective functions are also called one-to-one functions. This is a short video focusing on the proof.
From playlist Proofs

Proof synthesis and differential linear logic
Linear logic is a refinement of intuitionistic logic which, viewed as a functional programming language in the sense of the Curry-Howard correspondence, has an explicit mechanism for copying and discarding information. It turns out that, due to these mechanisms, linear logic is naturally r
From playlist Talks

11. Recursion Theorem and Logic
MIT 18.404J Theory of Computation, Fall 2020 Instructor: Michael Sipser View the complete course: https://ocw.mit.edu/18-404JF20 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP60_JNv2MmK3wkOt9syvfQWY Quickly reviewed last lecture. Discussed self-reference and the recur
From playlist MIT 18.404J Theory of Computation, Fall 2020

Distinguished Visitor Lecture Series Finding randomness Theodore A. Slaman University of California, Berkeley, USA
From playlist Distinguished Visitors Lecture Series

Theory of Computation 13. The Halting Problem aduni
From playlist [Shai Simonson]Theory of Computation

Computation Ep33, The Halting Problem (Apr 27, 2022)
This is a recording of a live class for Math 3342, Theory of Computation, an undergraduate course for math and computer science majors at Fairfield University, Spring 2022. The course is about finite automata, Turing machines, and related topics. Homework and handouts at the class websi
From playlist Math 3342 (Theory of Computation) Spring 2022

Nathalie Aubrun: About the Domino problem on finitely generated groups - Lecture 1
Abstract: Subshifts of finite type are of high interest from a computational point of view, since they can be described by a finite amount of information - a set of forbidden patterns that defines the subshift - and thus decidability and algorithmic questions can be addressed. Given an SFT
From playlist Mathematical Aspects of Computer Science

Stanford Seminar - Propositions as Types
"Propositions as Types" - Philip Wadler of University of Edinburgh About the talk: The principle of Propositions as Types links logic to computation. At first sight it appears to be a simple coincidence---almost a pun---but it turns out to be remarkably robust, inspiring the design of the
From playlist Engineering

Introduction to Direct Proofs: If n is even, then n squared is even
This video introduces the mathematical proof method of direct proof provides an example of a direct proof. mathispower4u.com
From playlist Symbolic Logic and Proofs (Discrete Math)

Theory of Computation: The Halting Problem
This video is for my Spring 2020 section of MA 342, for the class meeting on Tuesday April 21. Fast forward music is from "Now Get Busy" by the Beastie Boys, licensed Creative Commons Noncommercial Sampling Plus.
From playlist Math 342 (Theory of Computation) Spring 2020

The Halting Problem: Theory of Computation (Apr 28, 2021)
This is a recording of a live class for Math 3342, Theory of Computation, an undergraduate course for math & computer science majors at Fairfield University, Spring 2021. Download class notes from class website. Class website: http://cstaecker.fairfield.edu/~cstaecker/courses/2021s3342/
From playlist Math 3342 (Theory of Computation) Spring 2021

Bonus Livestream Session - Ethereum Basics
You've got questions about Ethereum? Get them answered in this Ethereum Basics Livestream session by aantonop. Timestamps (by Yes2Crypto) 0:00:30 Welcome from Andreas 0:01:14 Thank you to Community Builders 0:02:47 Video "thank you" from Community Builders 0:05:32 Moderation Policy 0:
From playlist English Subtitles - aantonop Videos with subtitles in English
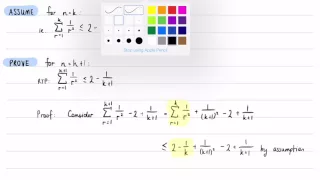
Inequality Proof: Summing Reciprocals of Squares (Experimental Silent Screencast)
via YouTube Capture
From playlist The Nature of Proof
