
Projection of One Vector onto Another Vector
Link: https://www.geogebra.org/m/wjG2RjjZ
From playlist Trigonometry: Dynamic Interactives!

Trig identities - What are they?
► My Trigonometry course: https://www.kristakingmath.com/trigonometry-course Trig identities are pretty tough for most people, because 1) there are so many of them, and 2) they’re hard to remember, and 3) it’s tough to recognize when you’re supposed to use them! But don’t worry, because
From playlist Trigonometry

From playlist Trigonometry TikToks

From playlist Trigonometry TikToks
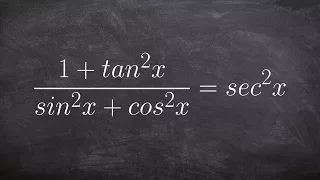
Use pythagorean identities to verify an identity
👉 Learn how to verify Pythagoras trigonometric identities. A Pythagoras trigonometric identity is a trigonometric identity of the form sin^2 (x) + cos^2 (x) or any of its derivations. To verify trigonometric expression means to verify that the term(s) on the left-hand side of the equality
From playlist Verify Trigonometric Identities
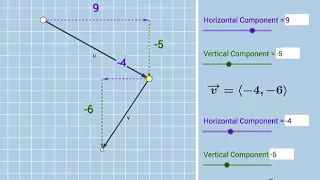
Adding Vectors Geometrically: Dynamic Illustration
Link: https://www.geogebra.org/m/tsBer5An
From playlist Trigonometry: Dynamic Interactives!

Using pythagorean identities to help me verify an identity
👉 Learn how to verify Pythagoras trigonometric identities. A Pythagoras trigonometric identity is a trigonometric identity of the form sin^2 (x) + cos^2 (x) or any of its derivations. To verify trigonometric expression means to verify that the term(s) on the left-hand side of the equality
From playlist Verify Trigonometric Identities


