
7F Diagonal Triangular Symmetric Matrices
Diagonal, triangular, and symmetric matrices.
From playlist Linear Algebra
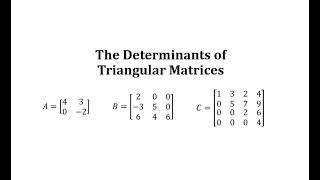
Determinants of Triangular Matrices
This video explains the short cut for finding determinants of triangular matrices.
From playlist The Determinant of a Matrix

Linear Algebra 14TBD: The Determinant of a Triangular Matrix
https://bit.ly/PavelPatreon https://lem.ma/LA - Linear Algebra on Lemma http://bit.ly/ITCYTNew - Dr. Grinfeld's Tensor Calculus textbook https://lem.ma/prep - Complete SAT Math Prep
From playlist Part 2 Linear Algebra: An In-Depth Course with a Focus on Applications

Linear Algebra 5.1.2 More About Eigenvectors and Eigenvalues
Proofs for Eigenvalues located on the main diagonal of a triangular matrix and for linear independence of eigenvectors.
From playlist Linear Algebra (Entire Course)

Linear Algebra for Computer Scientists. 12. Introducing the Matrix
This computer science video is one of a series of lessons about linear algebra for computer scientists. This video introduces the concept of a matrix. A matrix is a rectangular or square, two dimensional array of numbers, symbols, or expressions. A matrix is also classed a second order
From playlist Linear Algebra for Computer Scientists

Every operator on a finite-dimensional complex vector space has an upper-triangular matrix with respect to some basis. The eigenvalues of the operator are the numbers along the diagonal of this upper-triangular matrix.
From playlist Linear Algebra Done Right

Ring Theory: We define rings and give many examples. Items under consideration include commutativity and multiplicative inverses. Example include modular integers, square matrices, polynomial rings, quaternions, and adjoins of algebraic and transcendental numbers.
From playlist Abstract Algebra

An introduction to Invariant Theory - Harm Derksen
Optimization, Complexity and Invariant Theory Topic: An introduction to Invariant Theory Speaker: Harm Derksen Affiliation: University of Michigan Date: June 4, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

On eigenvectors of non-normal random matrices by Ofer Zeitouni
PROGRAM :UNIVERSALITY IN RANDOM STRUCTURES: INTERFACES, MATRICES, SANDPILES ORGANIZERS :Arvind Ayyer, Riddhipratim Basu and Manjunath Krishnapur DATE & TIME :14 January 2019 to 08 February 2019 VENUE :Madhava Lecture Hall, ICTS, Bangalore The primary focus of this program will be on the
From playlist Universality in random structures: Interfaces, Matrices, Sandpiles - 2019

Abstract Algebra | More examples involving rings: ideals and isomorphisms.
We give a few examples involving rings, one involving matrix rings and another involving the field of order 9. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Galois Representations 5 by Shaunak Deo
PROGRAM : ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (ONLINE) ORGANIZERS : Ashay Burungale (California Institute of Technology, USA), Haruzo Hida (University of California, Los Angeles, USA), Somnath Jha (IIT - Kanpur, India) and Ye Tian (Chinese Academy of Sciences, China) DA
From playlist Elliptic Curves and the Special Values of L-functions (ONLINE)

Darij Grinberg - The one-sided cycle shuffles in the symmetric group algebra
We study a new family of elements in the group ring of a symmetric group – or, equivalently, a class of ways to shuffle a deck of cards. Fix a positive integer n. Consider the symmetric group S_n. For each 1 ≤ ℓ ≤ n, we define an element t_ℓ := cyc_ℓ + cyc{ℓ,ℓ+1} + cyc_{ℓ,ℓ+1,ℓ+2} + · · ·
From playlist Combinatorics and Arithmetic for Physics: Special Days 2022

Dimitri Grigoryev - On a Tropical Version of the Jacobian Conjecture
We prove that, for a tropical rational map if for any point the convex hull of Jacobian matrices at smooth points in a neighborhood of the point does not contain singular matrices then the map is an isomorphism. We also show that a tropical polynomial map on the plane is an isomorphism if
From playlist Combinatorics and Arithmetic for Physics: 02-03 December 2020

Joel Kamnitzer - Symplectic Resolutions, Coulomb Branches, and 3d Mirror Symmetry 5/5
In the 21st century, there has been a great interest in the study of symplectic resolutions, such as cotangent bundles of flag varieties, hypertoric varieties, quiver varieties, and affine Grassmannian slices. Mathematicians, especially Braden-Licata-Proudfoot-Webster, and physicists obser
From playlist 2021 IHES Summer School - Enumerative Geometry, Physics and Representation Theory

Zero, identity, diagonal, triangular, banded matrices | Lecture 3 | Matrix Algebra for Engineers
Definition of the zero matrix, identity matrix, diagonal matrices, lower and upper triangular matrices and banded matrices. Join me on Coursera: https://www.coursera.org/learn/matrix-algebra-engineers Lecture notes at http://www.math.ust.hk/~machas/matrix-algebra-for-engineers.pdf Subs
From playlist Matrix Algebra for Engineers

Paul GUNNELLS - Cohomology of arithmetic groups and number theory: geometric, ... 1
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry) and connexion to number theory. The second part will deal with higher rank groups, mainly
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Frédéric Chapoton: Combinatorics and algebra of partially ordered sets - lecture 1
CIRM VIRTUAL EVENT Recorded during the meeting "French Computer Algebra Days" the March 03, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audio
From playlist Virtual Conference

An Introduction to Tensor Renormalization Group by Daisuke Kadoh
PROGRAM NONPERTURBATIVE AND NUMERICAL APPROACHES TO QUANTUM GRAVITY, STRING THEORY AND HOLOGRAPHY (HYBRID) ORGANIZERS: David Berenstein (University of California, Santa Barbara, USA), Simon Catterall (Syracuse University, USA), Masanori Hanada (University of Surrey, UK), Anosh Joseph (II
From playlist NUMSTRING 2022

What is a matrix? Free ebook http://tinyurl.com/EngMathYT
From playlist Intro to Matrices
