
Matthias Aschenbrenner: The algebra and model theory of transseries
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Jean-Morlet Chair - Hauser/Rond
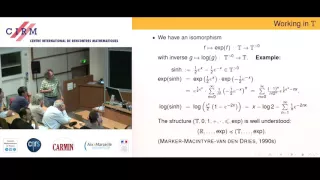
Lou van den Dries: The ordered differential field of transseries
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebra

Resurgence and Transseries in String Theory by Ricardo Schiappa
Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography DATE:27 January 2018 to 03 February 2018 VENUE:Ramanujan Lecture Hall, ICTS Bangalore The program "Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography" aims to
From playlist Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography

An intro to the core protocols of the Internet, including IPv4, TCP, UDP, and HTTP. Part of a larger series teaching programming. See codeschool.org
From playlist The Internet

Jean-Philippe Rolin : Logarithmico-exponential series and fractal analysis
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebra

GeoGebra 3D Calculator: When to Use?
GeoGebra 3D Calculator is one of the five apps in Calculator Suite. https://www.geogebra.org/calculator
From playlist GeoGebra Apps Intro: Which to USE?

Dimension and automorphisms in the differential (...) - M. Aschenbrenner - Workshop 2 - CEB T1 2018
Matthias Aschenbrenner (UCLA) / 05.03.2018 Dimension and automorphisms in the differential field of transseries. I plan to survey some of the pleasant properties enjoyed by (topological) dimension of definable sets in the differential field T of transseries; to explain what we know abou
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

Matthias Aschenbrenner 5/22/15 Part 2
Title: Model-Completeness of Transseries
From playlist Spring 2015

Matthias Aschenbrenner 5/22/15 Part 1
Title: Model-Completeness of Transseries
From playlist Spring 2015

Writing Equivalent Polar Coordinates Quiz
Link: https://www.geogebra.org/m/MxAvq5Yt
From playlist Trigonometry: Dynamic Interactives!
Link: https://www.geogebra.org/m/BGPxZHWy
From playlist Trigonometry: Dynamic Interactives!
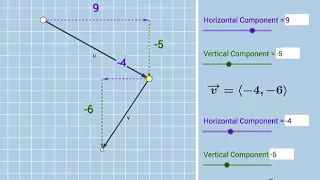
Adding Vectors Geometrically: Dynamic Illustration
Link: https://www.geogebra.org/m/tsBer5An
From playlist Trigonometry: Dynamic Interactives!

GeoGebra Scientific Calculator: When to Use?
GeoGebra Scientific Calculator is a free easy-to-use version of a standard handled scientific calculator. https://www.geogebra.org/scientific
From playlist GeoGebra Apps Intro: Which to USE?
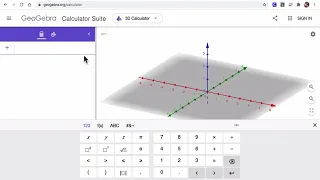
A very quick demo of how to access the 2D and 3D calculator on Geogebra.
From playlist Geogebra

Hydrodynamic attractors and applications (HYATT) by Michal P Heller
PROGRAM : THE MYRIAD COLORFUL WAYS OF UNDERSTANDING EXTREME QCD MATTER ORGANIZERS : Ayan Mukhopadhyay, Sayantan Sharma and Ravindran V DATE & TIME : 01 April 2019 to 17 April 2019 VENUE : Ramanujan Lecture Hall, ICTS Bangalore Strongly interacting phases of QCD matter at extreme tempera
From playlist The Myriad Colorful Ways of Understanding Extreme QCD Matter 2019

Projection of One Vector onto Another Vector
Link: https://www.geogebra.org/m/wjG2RjjZ
From playlist Trigonometry: Dynamic Interactives!

Patrick Speissegger, McMaster University A new Hardy field of relevance to Hilbert's 16th problem In our paper, we construct a Hardy field that embeds, via a map representing asymptotic expansion, into the field of transseries as described by Aschenbrenner, van den Dries and van der Hoev
From playlist Spring 2020 Kolchin Seminar in Differential Algebra

Ricardo Schiappa - Resurgence Asymptotics in String Theory
Following up on the morning lecture, I will give a very light introduction to resurgent asymptotics. These techniques will then be explored (again in the spirit of a light introduction) within transseries solutions of topological string theory, themselves obtained via a nonperturbative com
From playlist 7ème Séminaire Itzykson : « Résurgence et quantification »

