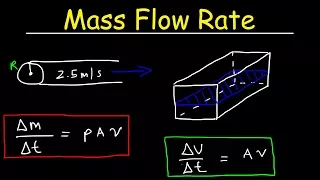
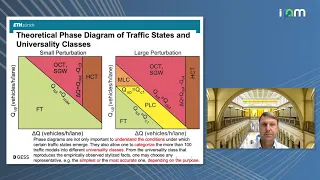
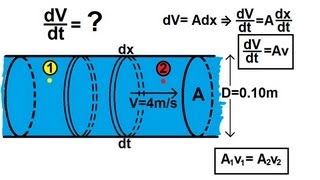
Conservation equations | Traffic flow
In mathematics and transportation engineering, traffic flow is the study of interactions between travellers (including pedestrians, cyclists, drivers, and their vehicles) and infrastructure (including highways, signage, and traffic control devices), with the aim of understanding and developing an optimal transport network with efficient movement of traffic and minimal traffic congestion problems. (Wikipedia).
Volume Flow Rate & Mass Flow Rate - Fluid Dynamics Physics Problems
This physics video tutorial provides a basic introduction into mass flow rate and volume flow rate. The mass flow rate is the change in mass per unit time. It is also equal to the product of the fluid density, cross sectional area and the speed of the fluid in a pipe. The volume flow ra
From playlist New Physics Video Playlist
Fluid flow with four points of curl interest
From playlist Curl
Linear Algebra - Lecture 14 - Applications to Networks
In this lecture, we study how to apply linear algebra techniques to flow networks.
From playlist Linear Algebra Lectures
Solving a Flow Rate Problem With and Without Conditions (No Roads Closed / 1 Road Closed)
This video provides an example on how to solve a flow rate problem.
From playlist Augmented Matrices
Physics - Fluid Dynamics (1 of 25) Viscosity & Fluid Flow: Introduction
Visit http://ilectureonline.com for more math and science lectures! In this video I will introduce viscosity and fluid flow involving frictional forces between the molecules and the containing walls. Next video in this series can be seen at: https://youtu.be/3xukKynwA70
From playlist PHYSICS 34 FLUID DYNAMICS
Traffic management in dense urban areas is an extremely complex problem with a host of conflicting goals and challenges. One of the most fundamental of those challenges happens at an intersection, where multiple streams of traffic - including vehicles, bikes and pedestrians - need to safel
From playlist Civil Engineering
Simone Göttlich: Traffic flow models with non-local flux and extensions to networks
We present a Godunov type numerical scheme for a class of scalar conservation laws with nonlocal flux arising for example in traffic flow modeling. The scheme delivers more accurate solutions than the widely used Lax-Friedrichs type scheme and also allows to show well-posedness of the mode
From playlist Numerical Analysis and Scientific Computing
Fluid flow for cos(x+y)i + sin(xy)j
From playlist Curl
The Problem of Traffic: A Mathematical Modeling Journey
How can we mathematically model traffic? Specifically we will study the problem of a single lane of cars and the perturbation from equilibrium that occurs when one car brakes, and that braking effect travels down the line of cars, amplifying as it goes along, due to the delayed reaction ti
From playlist Cool Math Series
Benjamin Seibold: "Energy Impact of Automated Vehicles used as Sparse Traffic Controllers"
Mathematical Challenges and Opportunities for Autonomous Vehicles 2020 Workshop II: Safe Operation of Connected and Autonomous Vehicle Fleets "Energy Impact of Automated Vehicles used as Sparse Traffic Controllers" Benjamin Seibold - Temple University, Mathematics Abstract: It is a popul
From playlist Mathematical Challenges and Opportunities for Autonomous Vehicles 2020
Benjamin Seibold: The Frustrating Beauty of Traffic Waves & How Automated Vehicles Can Prevent Them
IPAM Public Lecture 2020 “The Frustrating Beauty of Traffic Waves — And How Automated Vehicles Can Prevent Them” Benjamin Seibold - Temple University Abstract: A distinguishing feature of vehicular traffic flow is that it may exhibit significant wave patterns. This talk demonstrates tha
From playlist Mathematical Challenges and Opportunities for Autonomous Vehicles 2020
Paola Goatin: "Macroscopic models for Autonomous Vehicles"
Mathematical Challenges and Opportunities for Autonomous Vehicles Tutorials 2020 "Macroscopic models for Autonomous Vehicles" Paola Goatin - Inria Sophia Antipolis-Méditerranée Abstract: My lecture will give an introduction to macroscopic traffic flow models (first and second order), the
From playlist Mathematical Challenges and Opportunities for Autonomous Vehicles 2020
Benjamin Seibold: "Basic Traffic Models and Traffic Waves" (Part 1/2)
Watch part 2/2 here: https://youtu.be/tDzbGUBWtcI Mathematical Challenges and Opportunities for Autonomous Vehicles Tutorials 2020 "Basic Traffic Models and Traffic Waves" (Part 1/2) Benjamin Seibold - Temple University Institute for Pure and Applied Mathematics, UCLA September 16, 2020
From playlist Mathematical Challenges and Opportunities for Autonomous Vehicles 2020
Dirk Helbing: "Towards Digital Democracies & Societal Resilience: Upgrading Smart Cities with Co..."
Mathematical Challenges and Opportunities for Autonomous Vehicles 2020 Workshop IV: Social Dynamics beyond Vehicle Autonomy "Towards Digital Democracies and Societal Resilience: Upgrading Smart Cities with Collective Intelligence, and More" Dirk Helbing - ETH Zurich Abstract: Given the o
From playlist Mathematical Challenges and Opportunities for Autonomous Vehicles 2020
Our objective was to design road and traffic control systems that maximize traffic flow and minimize red-light wait time. Melvin Friedman describe how they found a way to relieve bumper-to-bumper traffic on highways and build inexpensive uninterrupted flow roads that function like highways
From playlist Wolfram Technology Conference 2020
Speaker: Elisa Jasinska I can feel your traffic The explosion of internet traffic is leading to higher bandwidths and an increased need for high speed networks. To analyze and optimize such networks an efficient monitoring system is required. The sFlow standard describes a mechanism to
From playlist 23C3: Who can you trust
Antonella Ferrara: "From connected & autonomous vehicles control to vehicular traffic control"
Mathematical Challenges and Opportunities for Autonomous Vehicles 2020 Workshop II: Safe Operation of Connected and Autonomous Vehicle Fleets "From connected and autonomous vehicles control to vehicular traffic control, a multi-scale perspective" Antonella Ferrara - Università di Pavia A
From playlist Mathematical Challenges and Opportunities for Autonomous Vehicles 2020
Dan Work: "Transportation Engineering for Connected and Automated Vehicles" (Part 1/2)
Watch part 2/2 here: https://youtu.be/yAi6OPt34jo Mathematical Challenges and Opportunities for Autonomous Vehicles Tutorials 2020 "Transportation Engineering for Connected and Automated Vehicles" (Part 1/2) Dan Work - Vanderbilt University Institute for Pure and Applied Mathematics, UC
From playlist Mathematical Challenges and Opportunities for Autonomous Vehicles 2020
Physics -Fluid Dynamics (1 of 2) Fluid Flow
Visit http://ilectureonline.com for more math and science lectures! In this video I will show you how to find the velocity fluid flow in a pipe.
From playlist PHYSICS 34 FLUID DYNAMICS
Benjamin Seibold: "Basic Traffic Models and Traffic Waves" (Part 2/2)
Watch part 1/2 here: https://youtu.be/9_1cEtimRNE Mathematical Challenges and Opportunities for Autonomous Vehicles Tutorials 2020 "Basic Traffic Models and Traffic Waves" (Part 2/2) Benjamin Seibold - Temple University Institute for Pure and Applied Mathematics, UCLA September 17, 2020
From playlist Mathematical Challenges and Opportunities for Autonomous Vehicles 2020