
Tight or release orange nut for clamping or repositioning green bar.
From playlist Mechanisms

Loose the screw for moving the stopper to new position and then tighten it. The stopper is kept immobile by wedge mechnism.
From playlist Mechanisms

This knot is very useful for adjusting tie downs quickly and easily. For example, a tarp could be held down by a series of these knots and be made very tight so the wind cannot make it rise, and easily be removed simply by sliding the knots later. A taut line knot is also used to keep larg
From playlist Practical Projects & Skills

Green tube and blue fixed jaw are fixed together. Tight or release grey nut for clamping or repositioning yellow tube. The green tube is cut off for easy understanding.
From playlist Mechanisms

Scientists tie tightest knot ever
New molecular knots like this one could mean stronger, more flexible polymers. Learn more: http://scim.ag/2jvPqz5
From playlist Materials and technology

Tight or release orange nut for clamping or repositioning violet and yellow tubes simultaneously. The yellow tube is released thanks to the flexibility of the white support. The part below the mechanism is the support, which is cut off half.
From playlist Mechanisms
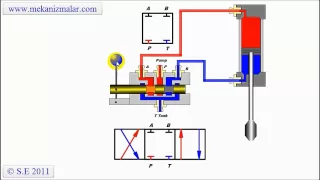
http://www.mekanizmalar.com This is a flash animation of a hydraulic closed center valve.
From playlist Pneumatic and Hydraulics

Alex Wright - Minicourse - Lecture 5
Alex Wright Dynamics, geometry, and the moduli space of Riemann surfaces We will discuss the GL(2,R) action on the Hodge bundle over the moduli space of Riemann surfaces. This is a very friendly action, because it can be explained using the usual action of GL(2,R) on polygons in the plane
From playlist Maryland Analysis and Geometry Atelier

P. Apisa - Marked points in genus two and beyond
In the principal stratum in genus two, McMullen observed that something odd happens - there is only one nonarithmetic Teichmuller curve - the one generated by the decagon. This strange phenomenon begets another - a primitive translation surface in genus two admits a periodic point that is
From playlist Ecole d'été 2018 - Teichmüller dynamics, mapping class groups and applications

Yoga with Olivia part 5 - Opening up tight shoulders
My friend Olivia has just opened up her own Holistic Health Clinic in Brisbane so I've invited her to come onto the channel to teach us some basic Yoga. In this video we specifically focus on a routine for tight shoulders. If you have tight shoulders, you would really enjoy this video. Try
From playlist Yoga

Complex geometry of Teichmuller domains (Lecture 2) by Harish Seshadri
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019

In this Wolfram Technology Conference presentation, Seth Chandler explores the practicalities of using J/Link to establish Mathematica as a communications hub among code developed in Clojure, Scala, and Jython. For more information about Mathematica, please visit: http://www.wolfram.com/m
From playlist Wolfram Technology Conference 2012

Stanford Seminar - Opening the Doors of (Robot) Perception - Luca Carlone
Opening the Doors of (Robot) Perception: Towards Certifiable Spatial Perception Algorithms and Systems Luca Carlone MIT February 11, 2022 Spatial perception —the robot’s ability to sense and understand the surrounding environment— is a key enabler for autonomous systems operating in co
From playlist Stanford AA289 - Robotics and Autonomous Systems Seminar

Why do shoelaces untie themselves?
Failure to stay knotty is a two-stage process according to a new study of lace mechanics. Learn more: http://scim.ag/2oVypF9
From playlist Materials and technology

Kimihiko Motegi: L-space knots in twist families and satellite L-space knots
Abstract: Twisting a knot K in S3 along a disjoint unknot c produces a twist family of knots {Kn} indexed by the integers. Comparing the behaviors of the Seifert genus g(Kn) and the slice genus g4(Kn) under twistings, we prove that if g(Kn)−g4(Kn) [is less than] C for some constant C for i
From playlist Topology

Billiards in quadrilaterals, Hurwitz spaces, and real multiplication of Hecke type - Alex Wright
Members' Seminar Topic: Billiards in quadrilaterals, Hurwitz spaces, and real multiplication of Hecke type Speaker: Alexander Wright Affiliation: Stanford University; Member, School of Mathematics Monday, November 30 Video Link: https://video.ias.edu/membsem/2015/1130-Wright After a brief
From playlist Mathematics

Vyacheslav Egorov: invokedynamic.js | JSConf EU 2014
The apple always falls down attracted by the gravity of the earth. It’s the law of physics. The function is never inlined if it’s source is bigger than 600 characters long. It’s a heuristic - a physical law of our dystopian cyber-world confined inside a JavaScript Virtual Machine. Ever wa
From playlist JSConf EU 2014

New Results on Projections - Guy Moshkovitz
Computer Science/Discrete Mathematics Seminar II Topic: New Results on Projections Speaker: Guy Moshkovitz Affiliation: Member, School of Mathematics Date: January 22, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

Taper Tooling Tightening Fixture
Short project / long overdue: taper tooling tightening fixture -- say that 5 times fast. -------------------------------- Music: Pink Lemonade - Silent Partner
From playlist All Uploads
