
Abstract Algebra | First Isomorphism Theorem for Rings
We present a proof of the first isomorphism theorem for rings. http://www.michael-penn.net https://www.researchgate.net/profile/Michael_Penn5 http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Now that we know what quotient groups, a kernel, and normal subgroups are, we can look at the first isomorphism theorem. It states that the quotient group created by the kernel of a homomorphism is isomorphic to the (second) group in the homomorphism.
From playlist Abstract algebra

First Isomorphism Theorem (podcast style)
Created by Erik Davis and Jordy Lopez
From playlist Summer of Math Exposition Youtube Videos

Abstract Algebra | First Isomorphism Theorem for Groups
We state and prove the first isomorphism theorem for groups. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra
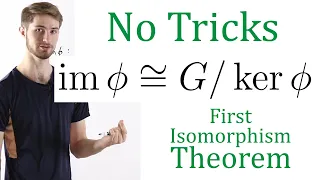
A Natural Proof of the First Isomorphism Theorem (Group Theory)
The first isomorphism theorem is one of the most important theorems in group theory, but the standard proof may seem artificial, like every step of the proof is set up knowing that we're trying to create an isomorphism. In this video, we show an alternate proof with no such tricks using th
From playlist Group Theory
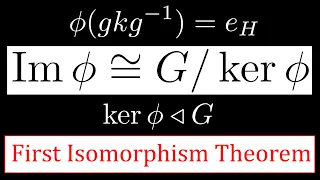
Kernel and First Isomorphism Theorem - Group Theory
0:00 Kernel is a Normal Subgroup 5:20 First Isomorphism Theorem The first isomorphism theorem is a fundamental theorem in group theory that gives us a powerful way to find isomorphic groups. In this video, we explain what the kernel of a homomorphism is and how to turn a homomorphism into
From playlist Group Theory

First Fundamental Theorem of Calculus Calculus 1 AB
I introduce and define the First Fundamental Theorem of Calculus. I finish by working through 4 examples involving Polynomials, Quotients, Radicals, Absolute Value Function, and Trigonometric Functions. Check out http://www.ProfRobBob.com, there you will find my lessons organized by clas
From playlist Calculus

Zack Sylvan - Doubling stops & spherical swaps
June 28, 2018 - This talk was part of the 2018 RTG mini-conference Low-dimensional topology and its interactions with symplectic geometry
From playlist 2018 RTG mini-conference on low-dimensional topology and its interactions with symplectic geometry II

Simple groups, Lie groups, and the search for symmetry II | Math History | NJ Wildberger
This is the second video in this lecture on simple groups, Lie groups and manifestations of symmetry. During the 19th century, the role of groups shifted from its origin in number theory and the theory of equations to its role in describing symmetry in geometry. In this video we talk abou
From playlist MathHistory: A course in the History of Mathematics

Erin Chambers (2/5/19): Computing optimal homotopies
Abstract: The question of how to measure similarity between curves in various settings has received much attention recently, motivated by applications in GIS data analysis, medical imaging, and computer graphics. Geometric measures such as Hausdorff and Fr\'echet distance have efficient al
From playlist AATRN 2019

Introduction to Number Theory, Part 1: Divisibility
The first video in a series about elementary number theory, following the book by Underwood Dudley. We define the basic concept of divisibility, and prove a fundamental lemma. Intro:(0:00) Definition of Divisibility:(6:40) Our First Theorem:(9:00)
From playlist Introduction to Number Theory

Microlocal Theory of Sheaves and Applications to Non-Displaceability - Pierre Schapira
Pierre Schapira University of Paris 6, France January 31, 2011 I will explain the main notions of the microlocal theory of sheaves: the microsupport and its behaviour with respect to the operations, with emphasis on the Morse lemma for sheaves. Then, inspired by the recent work of Tamarkin
From playlist Mathematics

Priyam Patel: Mapping class groups of infinite-type surfaces and their actions on hyperbolic graphs
CONFERENCE Recording during the thematic meeting : "Big Mapping Class Group and Diffeomorphism Groups " the October 11, 2022 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mat
From playlist Topology

John Milnor - The Abel Prize interview 2011
02:33 Beginnings, Aptitude, "socially maladjusted" 03:40 Putnam, Math. as problem-solving 04:10 First paper (at 18 yo) 06:10 John Nash, Princeton 07:45 games: Kriegspiel, Go, Nash 09:25 game theory 10:35 knot theory, Papakyriakopoulos 15:45 manifolds 17:55 dim. 7 manifolds 20:35 collaborat
From playlist The Abel Prize Interviews

Introduction of Theravada Buddhism to Angkor, Cambodia – Mapping Through the Archaeological Record
How do we identify religious transition and social change in the archaeological record? How does an entire society seamlessly, or not so seamlessly, adopt an entirely new worldview? Is it gradual, or immediate, and what are the consequences? And of earlier traditions, what remains, what is
From playlist Council on Southeast Asia Studies (CSEAS)

Claude Viterbo - Théorie des faisceaux et Topologie symplectique (Part 2)
L’utilisation de méthodes de théorie des faisceaux (Kashiwara-Schapira)a été dévelopée ces dernières années par Tamarkin, Nadler, Zaslow, Guillermou, Kashiwara et Schapira. Nous essaierons d’en donner un aperçu à la fois pour démontrer des résultats classiques, comme la conjecture d’Arnold
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications

Paul Turner: A hitchhiker's guide to Khovanov homology - Part I
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Geometry

Abstract Algebra - 10.2 The First Isomorphism Theorem
We complete Chapter 10 by examining the First Isomorphism Theorem. This theorem connects what we know about Factor Groups to what we know about isomorphisms and homomorphisms. Video Chapters: Intro 0:00 First Isomorphism Theorem 0:06 More From the First Isomorphism Theorem 7:23 Practice
From playlist Abstract Algebra - Entire Course

Stéphane Guillermou - Microlocal sheaf theory and symplectic geometry
Abstract: The microlocal theory of sheaves has been introduced and developed by Kashiwara and Schapira in the 80’s, with motivations coming from the theory of D-modules. It has been applied some years ago to the study of symplectic geometry of cotangent bundles in papers of Nadler-Zaslow
From playlist Algebraic Analysis in honor of Masaki Kashiwara's 70th birthday
