
Math 101 091317 Introduction to Analysis 06 Introduction to the Least Upper Bound Axiom
Definition of the maximum (minimum) of a set. Existence of maximum and minimum for finite sets. Definitions: upper bound of a set; bounded above; lower bound; bounded below; bounded. Supremum (least upper bound); infimum (greatest lower bound). Statement of Least Upper Bound Axiom (com
From playlist Course 6: Introduction to Analysis (Fall 2017)

Math 101 Introduction to Analysis 091815: Least Upper Bound Axiom
The least upper bound axiom. Maximum and minimum of a set of real numbers. Upper bound; lower bound; bounded set. Least upper bound; greatest lower bound.
From playlist Course 6: Introduction to Analysis

Number Theory - Fundamental Theorem of Arithmetic
Fundamental Theorem of Arithmetic and Proof. Building Block of further mathematics. Very important theorem in number theory and mathematics.
From playlist Proofs
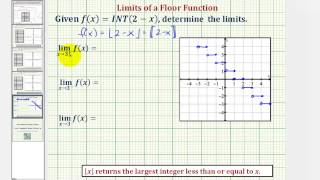
Ex: Limits of the Floor Function (Greatest Integer Function)
This video explains how to determine limits of a floor function graphically and numerically using a graphing calculator. Site: http://mathispower4u.com
From playlist Limits

Ex: Limits Involving the Greatest Integer Function
This video provides four examples of how to determine limits of a greatest integer function. Site: http://mathispower4u.com
From playlist Limits

Math 101 091517 Introduction to Analysis 07 Consequences of Completeness
Least upper bound axiom implies a "greatest lower bound 'axiom'": that any set bounded below has a greatest lower bound. Archimedean Property of R.
From playlist Course 6: Introduction to Analysis (Fall 2017)

Shrawan Kumar: Root components for tensor product of affine Kac-Moody Lie algebra modules
SMRI Algebra and Geometry Online: Shrawan Kumar (University of North Carolina) Abstract: This is a joint work with Samuel Jeralds. Let 𝔤 be an affine Kac-Moody Lie algebra and let λ, µ be two dominant integral weights for 𝔤. We prove that under some mild restriction, for any positive root
From playlist SMRI Algebra and Geometry Online

Verlinde Dimension Formula for the Space of Conformal Blocks and the moduli of G-bundles
Verlinde Dimension Formula Topic: Verlinde Dimension Formula for the Space of Conformal Blocks and the moduli of G-bundles Speaker: Shrawan Kumar Affiliation: University of North Carolina; Member, School of Mathematics
From playlist Verlinde Dimension Formula

Introduction to quantized enveloping algebras - Leonardo Maltoni
Quantum Groups Seminar Topic: Introduction to quantized enveloping algebras Speaker: Leonardo Maltoni Affiliation: Sorbonne University Date: January 28, 2021 For more video please visit http://video.ias.edu
From playlist Quantum Groups Seminar

Geordie Williamson: Langlands and Bezrukavnikov II Lecture 9
SMRI Seminar Series: 'Langlands correspondence and Bezrukavnikov’s equivalence' Geordie Williamson (University of Sydney) Abstract: The second part of the course focuses on affine Hecke algebras and their categorifications. Last year I discussed the local Langlands correspondence in bro
From playlist Geordie Williamson: Langlands correspondence and Bezrukavnikov’s equivalence

A gentle introduction to group representation theory -Peter Buergisser
Optimization, Complexity and Invariant Theory Topic: A gentle introduction to group representation theory Speaker: Peter Buergisser Affiliation: Technical University of Berlin Date: June 4, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Mumford-Tate Groups and Domains - Phillip Griffiths
Phillip Griffiths Professor Emeritus, School of Mathematics March 28, 2011 For more videos, visit http://video.ias.edu
From playlist Mathematics

Ilya Dumanski - Schubert varieties in the Beilinson-Drinfeld Grassmannian
Ilya Dumanski (MIT) The Borel-Weil theorem states that the space of sections of a certain line bundle on the flag variety is isomorphic to the irreducible representation of the corresponding reductive group. The classical result of Demazure describes the restriction of sections to the Sch
From playlist Azat Miftakhov Days Against the War

Geordie Williamson: Langlands and Bezrukavnikov II Lecture 20
SMRI Seminar Series: 'Langlands correspondence and Bezrukavnikov’s equivalence' Geordie Williamson (University of Sydney) Abstract: The second part of the course focuses on affine Hecke algebras and their categorifications. Last year I discussed the local Langlands correspondence in bro
From playlist Geordie Williamson: Langlands correspondence and Bezrukavnikov’s equivalence

Least Upper Bound Property In this video, I state the least upper bound property and explain what makes the real numbers so much better than the rational numbers. It's called Real Analysis after all! Check out my Real Numbers Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmCZ
From playlist Real Numbers
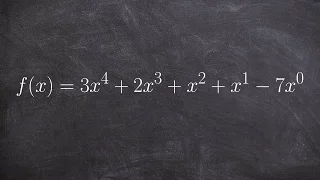
What is the definition of standard form, degree and leading coefficient of a polynomial
👉 Learn how to find the degree and the leading coefficient of a polynomial expression. The degree of a polynomial expression is the the highest power (exponent) of the individual terms that make up the polynomial. For terms with more that one variable, the power (exponent) of the term is t
From playlist Find the leading coefficient and degree of a polynomial | equation

Verlinde Dimension Formula for the Space of Conformal Blocks and the moduli of... - Shrawan Kumar
Verlinde Dimension Formula Topic: Verlinde Dimension Formula for the Space of Conformal Blocks and the moduli of G-bundles Speaker: Shrawan Kumar Affiliation: University of North Carolina; Member, School of Mathematics Date: October 13, 2022
From playlist Mathematics

Proof of a 35 Year Old Conjecture for Entropy of Coherent States and Generalization - Elliot Lieb
Elliot Lieb Princeton University November 12, 2012 35 years ago Wehrl defined a classical entropy of a quantum density matrix using Gaussian (Schr\"odinger, Bargmann, ...) coherent states. This entropy, unlike other classical approximations, has the virtue of being positive. He conjectured
From playlist Mathematics

How to find the degree and leading coefficient of a polynomial (mistake)
👉 Learn how to find the degree and the leading coefficient of a polynomial expression. The degree of a polynomial expression is the highest power (exponent) of the individual terms that make up the polynomial. For terms with more that one variable, the power (exponent) of the term is the s
From playlist Find the leading coefficient and degree of a polynomial | expression
