Tensor product model transformation

Control theory

In mathematics, the tensor product (TP) model transformation was proposed by Baranyi and Yam as key concept for higher-order singular value decomposition of functions. It transforms a function (which can be given via closed formulas or neural networks, fuzzy logic, etc.) into TP function form if such a transformation is possible. If an exact transformation is not possible, then the method determines a TP function that is an approximation of the given function. Hence, the TP model transformation can provide a trade-off between approximation accuracy and complexity. A free MATLAB implementation of the TP model transformation can be downloaded at [1] or an old version of the toolbox is available at MATLAB Central [2]. A key underpinning of the transformation is the higher-order singular value decomposition. Besides being a transformation of functions, the TP model transformation is also a new concept in qLPV based control which plays a central role in the providing a valuable means of bridging between identification and polytopic systems theories. The TP model transformation is uniquely effective in manipulating the convex hull of polytopic forms, and, as a result has revealed and proved the fact that convex hull manipulation is a necessary and crucial step in achieving optimal solutions and decreasing conservativeness in modern LMI based control theory. Thus, although it is a transformation in a mathematical sense, it has established a conceptually new direction in control theory and has laid the ground for further new approaches towards optimality. Further details on the control theoretical aspects of the TP model transformation can be found here: TP model transformation in control theory. The TP model transformation motivated the definition of the "HOSVD canonical form of TP functions", on which further information can be found here. It has been proved that the TP model transformation is capable of numerically reconstructing this HOSVD based canonical form. Thus, the TP model transformation can be viewed as a numerical method to compute the HOSVD of functions, which provides exact results if the given function has a TP function structure and approximative results otherwise. The TP model transformation has recently been extended in order to derive various types of convex TP functions and to manipulate them. This feature has led to new optimization approaches in qLPV system analysis and design, as described at TP model transformation in control theory. (Wikipedia).

A Concrete Introduction to Tensor Products

The tensor product of vector spaces (or modules over a ring) can be difficult to understand at first because it's not obvious how calculations can be done with the elements of a tensor product. In this video we give an explanation of an explicit construction of the tensor product and work

From playlist Tensor Products

Lecture 27. Properties of tensor products

0:00 Use properties of tensor products to effectively think about them! 0:50 Tensor product is symmetric 1:17 Tensor product is associative 1:42 Tensor product is additive 21:40 Corollaries 24:03 Generators in a tensor product 25:30 Tensor product of f.g. modules is itself f.g. 32:05 Tenso

From playlist Abstract Algebra 2

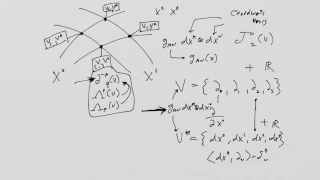
What is a Tensor? Lesson 29: Transformations of tensors and p-forms (part review)

What is a Tensor? Lesson 29: Tensor and N-form Transformations This long lesson begins with a review of tensor product spaces and the relationship between coordinate transformations on spacetime and basis transformations of tensor fields. Then we do a full example to introduce the idea th

From playlist What is a Tensor?

The TRUTH about TENSORS, part 5: ... is something that transforms like a tensor

In the longest video of this series (yet), we review contravariant and covariant vectors, and deriving the transformation law for a multi-linear map on a repeated tensor product of a vector space and its dual. Introduction (0:00) Contravariant vectors (1:33) Dual space (10:24) The transfo

From playlist The TRUTH about TENSORS

What is a Tensor? Lesson 30: Transformation of forms - formal study (Part I)

From playlist What is a Tensor?

What is a Tensor 5: Tensor Products

What is a Tensor 5: Tensor Products Errata: At 22:00 I write down "T_00 e^0 @ e^1" and the correct expression is "T_00 e^0 @ e^0"

From playlist What is a Tensor?

What is a Tensor 6: Tensor Product Spaces

What is a Tensor 6: Tensor Product Spaces There is an error at 15:00 which is annotated but annotations can not be seen on mobile devices. It is a somewhat obvious error! Can you spot it? :)

From playlist What is a Tensor?

RT9. Basic Tensor Analysis

Representation Theory: We apply character theory to tensor products. We obtain a character formula for general tensor products and, as special cases, alternating and symmetric 2-tensors. As an application, we compute the character table for S4, the symmetric group on 4 letters.

From playlist Representation Theory

Tensor Analysis and Applications

Tensors are used in various areas of mathematics and physics, particularly in theoretical calculations involving fields in vector spaces. The Einstein's summation convention implies summation over the dummy indices that appear twice in a term as in matrix-matrix or matrix-vector products.

From playlist Wolfram Technology Conference 2021

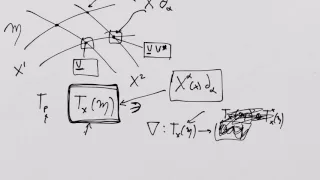
What is a Tensor? Lesson 16: The metric tensor field

From playlist What is a Tensor?

Visu Makam: "Maximum Likelihood Estimation for Tensor Normal Models"

Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021 Workshop IV: Efficient Tensor Representations for Learning and Computational Complexity "Maximum Likelihood Estimation for Tensor Normal Models" Visu Makam - Institute for Advanced Study Abstract: We study sa

From playlist Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021

Jason Morton: "An Algebraic Perspective on Deep Learning, Pt. 1"

Graduate Summer School 2012: Deep Learning, Feature Learning "An Algebraic Perspective on Deep Learning, Pt. 1" Jason Morton, Pennsylvania State University Institute for Pure and Applied Mathematics, UCLA July 19, 2012 For more information: https://www.ipam.ucla.edu/programs/summer-scho

From playlist GSS2012: Deep Learning, Feature Learning

Catherine Meusburger: Turaev-Viro State sum models with defects

Talk by Catherine Meusburger in Global Noncommutative Geometry Seminar (Europe) http://www.noncommutativegeometry.nl/ncgseminar/ on March 17, 2021

From playlist Global Noncommutative Geometry Seminar (Europe)

Tensor Network Renormalization - G. Vidal - 2/24/2015

Introduction by John Preskill. Learn more about the Inaugural Celebration and Symposium of the Walter Burke Institute for Theoretical Physics: https://burkeinstitute.caltech.edu/workshops/Inaugural_Symposium Produced in association with Caltech Academic Media Technologies. ©2015 Californ

From playlist Walter Burke Institute for Theoretical Physics - Dedication and Inaugural Symposium - Feb. 23-24, 2015

Anna Seigal: "Tensors in Statistics and Data Analysis"

Watch part 1/2 here: https://youtu.be/9unKtBoO5Hw Tensor Methods and Emerging Applications to the Physical and Data Sciences Tutorials 2021 "Tensors in Statistics and Data Analysis" Anna Seigal - University of Oxford Abstract: I will give an overview of tensors as they arise in settings

From playlist Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021

Speed up your Cosine Similarity for SBERT sentence embeddings via Sentence Transformers (SBERT 17)

Code shows speed improvements in COLAB for cosine similarity for SBERT: (a) new & improved pre-trained SentenceTransformer models (HuggingFace) and (b) utilizing normalized tensors with dot product instead of cosine similarity operators for SBERT sentence embeddings. Beware of model spec

From playlist SBERT: Python Code Sentence Transformers: a Bi-Encoder /Transformer model #sbert

Evrim Acar - Constrained Multimodal Data Mining using Coupled Matrix and Tensor Factorizations

Recorded 11 January 2023. Evrim Acar of Simula Research Laboratory presents "Extracting Insights from Complex Data: Constrained Multimodal Data Mining using Coupled Matrix and Tensor Factorizations" at IPAM's Explainable AI for the Sciences: Towards Novel Insights Workshop. Abstract: In or

From playlist 2023 Explainable AI for the Sciences: Towards Novel Insights

Automorphism group of the moduli space of parabolic vector bundles by David Alfaya Sanchez

DISCUSSION MEETING ANALYTIC AND ALGEBRAIC GEOMETRY DATE:19 March 2018 to 24 March 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore. Complex analytic geometry is a very broad area of mathematics straddling differential geometry, algebraic geometry and analysis. Much of the interactions be

From playlist Analytic and Algebraic Geometry-2018

Proof: Uniqueness of the Tensor Product

Universal property introduction: https://youtu.be/vZzZhdLC_YQ This video proves the uniqueness of the tensor product of vector spaces (or modules over a commutative ring). This uses the universal property of the tensor product to prove the existence of an isomorphism (linear bijection) be

From playlist Tensor Products

Thomas KRAJEWSKI - Connes-Kreimer Hopf Algebras...

Connes-Kreimer Hopf Algebras : from Renormalisation to Tensor Models and Topological Recursion At the turn of the millenium, Connes and Kreimer introduced Hopf algebras of trees and graphs in the context of renormalisation. We will show how the latter can be used to formulate the analogu

From playlist Algebraic Structures in Perturbative Quantum Field Theory: a conference in honour of Dirk Kreimer's 60th birthday

Tensor product model transformation

Related pages