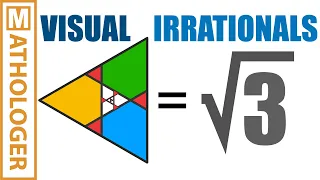
Visualising irrationality with triangular squares
NEW (Christmas 2019). Two ways to support Mathologer Mathologer Patreon: https://www.patreon.com/mathologer Mathologer PayPal: paypal.me/mathologer (see the Patreon page for details) Get ready for some brand new and very pretty visual proofs of the fact that root 2, root 3, root 5 and r
From playlist Recent videos

Calculus 5.3 The Fundamental Theorem of Calculus
My notes are available at http://asherbroberts.com/ (so you can write along with me). Calculus: Early Transcendentals 8th Edition by James Stewart
From playlist Calculus

Robert Bilder - What is Self Awareness?
'Self awareness' has a simple definition: the mental activity that reflects back on itself, the mental process of being aware of oneself being aware. Is self-awareness a uniquely human trait? Some animals seem to disagree. The deep significance of self-awareness is how on earth can physica
From playlist The Mind-Body Problem - Closer To Truth - Core Topic

Robert Bilder - How Does Memory Work?
We all wish for better memories. But how are memories stored? For all our neuroscience, we still do not know even the level in the brain where memories are stored—from inside neurons to long brain circuits. We do know that the synapses between neurons in the brain are critical, but how tho
From playlist How Does Memory Work? - CTT Interview Series

Theory of numbers: Congruences: Euler's theorem
This lecture is part of an online undergraduate course on the theory of numbers. We prove Euler's theorem, a generalization of Fermat's theorem to non-prime moduli, by using Lagrange's theorem and group theory. As an application of Fermat's theorem we show there are infinitely many prim
From playlist Theory of numbers

Introduction to additive combinatorics lecture 10.8 --- A weak form of Freiman's theorem
In this short video I explain how the proof of Freiman's theorem for subsets of Z differs from the proof given earlier for subsets of F_p^N. The answer is not very much: the main differences are due to the fact that cyclic groups of prime order do not have lots of subgroups, so one has to
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Robert Bilder - When Brains Go Bad
How do injured brains help explain normal brains? One of the most powerful ways of learning about normal brain function is to examine what functions are lost when parts or areas of the brain are degraded or destroyed due to injury or disease. The subtle variations of different brain proble
From playlist Understanding the Brain - Closer To Truth - Core Topics

Robert Bilder - How Do Brains Act?
Brains are the most complex organization of matter in the universe (as far as we know). What astonishing capacities are backed into such a small volume of warm, wet tissue—roughly three pounds, less than an average cantaloupe. What are the basic principles of brain function? How do they wo
From playlist Understanding the Brain - Closer To Truth - Core Topics

How Does Personal Identity Persist Through Time? | Episode 1205 | Closer To Truth
How do identity and consciousness persist through time? Is the self an illusion? Decades roll by; every molecule of our bodies changes many times. Yet our sense of self remains the same; continuous, a unity. How can this be? Featuring interviews with Simon Blackburn, Stephen Law, Richard S
From playlist Closer To Truth | Season 12

Calculus - The Fundamental Theorem, Part 1
The Fundamental Theorem of Calculus. First video in a short series on the topic. The theorem is stated and two simple examples are worked.
From playlist Calculus - The Fundamental Theorem of Calculus

Introduction to additive combinatorics lecture 1.8 --- Plünnecke's theorem
In this video I present a proof of Plünnecke's theorem due to George Petridis, which also uses some arguments of Imre Ruzsa. Plünnecke's theorem is a very useful tool in additive combinatorics, which implies that if A is a set of integers such that |A+A| is at most C|A|, then for any pair
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Multivariable Calculus | The Squeeze Theorem
We calculate a limit using a multivariable version of the squeeze theorem. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Multivariable Calculus

Differential Equations | Application of Abel's Theorem Example 2
We give an example of applying Abel's Theorem to construct a second solution to a differential equation given one solution. www.michael-penn.net
From playlist Differential Equations

Differential Equations | Abel's Theorem
We present Abel's Theorem with a proof. http://www.michael-penn.net
From playlist Differential Equations

Theory of numbers: Gauss's lemma
This lecture is part of an online undergraduate course on the theory of numbers. We describe Gauss's lemma which gives a useful criterion for whether a number n is a quadratic residue of a prime p. We work it out explicitly for n = -1, 2 and 3, and as an application prove some cases of Di
From playlist Theory of numbers

Calculus 1 (Stewart) Ep 22, Mean Value Theorem (Oct 28, 2021)
This is a recording of a live class for Math 1171, Calculus 1, an undergraduate course for math majors (and others) at Fairfield University, Fall 2021. The textbook is Stewart. PDF of the written notes, and a list of all episodes is at the class website. Class website: http://cstaecker.f
From playlist Math 1171 (Calculus 1) Fall 2021

Equidistribution of Unipotent Random Walks on Homogeneous spaces by Emmanuel Breuillard
PROGRAM : ERGODIC THEORY AND DYNAMICAL SYSTEMS (HYBRID) ORGANIZERS : C. S. Aravinda (TIFR-CAM, Bengaluru), Anish Ghosh (TIFR, Mumbai) and Riddhi Shah (JNU, New Delhi) DATE : 05 December 2022 to 16 December 2022 VENUE : Ramanujan Lecture Hall and Online The programme will have an emphasis
From playlist Ergodic Theory and Dynamical Systems 2022

What is Green's theorem? Chris Tisdell UNSW
This lecture discusses Green's theorem in the plane. Green's theorem not only gives a relationship between double integrals and line integrals, but it also gives a relationship between "curl" and "circulation". In addition, Gauss' divergence theorem in the plane is also discussed, whic
From playlist Vector Calculus @ UNSW Sydney. Dr Chris Tisdell

Real Analysis Ep 32: The Mean Value Theorem
Episode 32 of my videos for my undergraduate Real Analysis course at Fairfield University. This is a recording of a live class. This episode is more about the mean value theorem and related ideas. Class webpage: http://cstaecker.fairfield.edu/~cstaecker/courses/2020f3371/ Chris Staecker
From playlist Math 3371 (Real analysis) Fall 2020

What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics