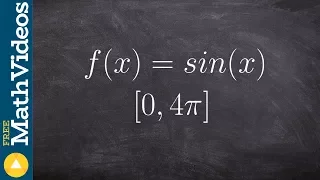
How to determine the max and min of a sine on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions
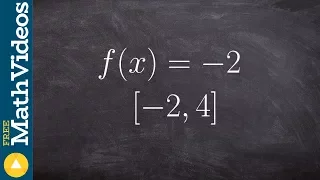
What is the max and min of a horizontal line on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Mod-06 Lec-35 Lyapunov Function Continued
Ordinary Differential Equations and Applications by A. K. Nandakumaran,P. S. Datti & Raju K. George,Department of Mathematics,IISc Bangalore.For more details on NPTEL visit http://nptel.ac.in.
From playlist IISc Bangalore: Ordinary Differential Equations and Applications | CosmoLearning.org Mathematics

Apply the EVT to the square function
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions
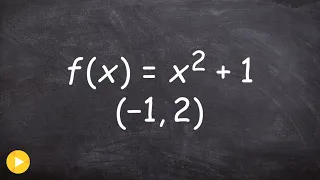
How to determine the absolute max min of a function on an open interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Peter Benner: Matrix Equations and Model Reduction, Lecture 5
Peter Benner from the Max Planck Institute presents: Matrix Equations and Model Reduction; Lecture 5
From playlist Gene Golub SIAM Summer School Videos

Determine the extrema of a function on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Who cares about the history of science?
The 2015 Wilkins-Bernal-Medawar Lecture was this year presented by Professor Hasok Chang, Hans Rausing professor of History and Philosophy of Science at the University of Cambridge. He looks at how we can learn from the radically different ways in which scientists have made sense of the u
From playlist Latest talks and lectures

How to evaluate the limit of a function by observing its graph
👉 Learn how to evaluate the limit of an absolute value function. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The absolute value function is a function which only takes the positive val
From playlist Evaluate Limits of Absolute Value

👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

On the number of ordinary lines determined by sets in complex space - Shubhangi Saraf
Computer Science/Discrete Mathematics Seminar I Topic: On the number of ordinary lines determined by sets in complex space Speaker: Shubhangi Saraf Affiliation: Rutgers University Date: December 5, 2016 For more video, visit http://video.ias.edu
From playlist Mathematics

Seminar In the Analysis and Methods of PDE (SIAM PDE): Alexander Kiselev
Title: The Flow of Polynomial Roots Under Differentiation Date: Thursday, June 2, 2022, 11:30 am EDT Speaker: Alexander Kiselev, Duke University Abstract: The question of how roots of polynomials move under differentiation is classical. Contributions to this subject have been made by Gaus
From playlist Seminar In the Analysis and Methods of PDE (SIAM PDE)
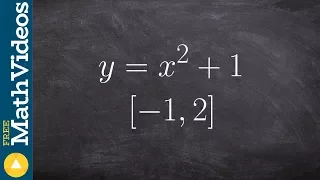
Find the max and min from a quadratic on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

David Sylvester: The Making of an Art Critic 1941-1956
John-Paul Stonard (Independent Scholar) The art critic David Sylvester (1924-2001) launched his career during the Second World War, writing for Tribune Magazine, and meeting artists and writers in London during the Blitz. His experiences, which can be reconstructed from his own unpublished
From playlist "In the Same Boat”: British and American Visual Culture During the Second World War

Sylvester-Gallai Problem for Quadratic Polynomials by Shir Peleg-Schatzman
Discussion Meeting Workshop on Algebraic Complexity Theory  ORGANIZERS Prahladh Harsha, Ramprasad Saptharishi and Srikanth Srinivasan DATE & TIME 25 March 2019 to 29 March 2019 VENUE Madhava Lecture Hall, ICTS Bangalore Algebraic complexity aims at understanding the computationa
From playlist Workshop on Algebraic Complexity Theory 2019

Sparse resultants in differential and difference algebra: an overview
From playlist Workshop on Model Theory, Differential/Difference Algebra, and Applications
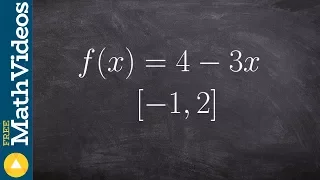
Find the max and min of a linear function on the closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Guillaume Moroz: Computational real algebraic geometry and applications to robotics - lecture 2
Guillaume MCIRM VIRTUAL EVENT Recorded during the meeting "French Computer Algebra Days" the March 04, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on C
From playlist Virtual Conference

Determine the extrema using the end points of a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions
