
In the first mini-lecture, we ask the question: what is surface anatomy? We learn how anatomy is the study of the structure of our bodies, including osteology, histology, gross anatomy, imaging, embryology and indeed surface anatomy. As you might imagine, surface anatomy studies the extern
From playlist Biology

Confessions of a surface plate abuser
In this video we make a round cast iron sanding plate for detailing machined parts out of an off cut disc of cast iron. Contrary to popular shop practice using a precision surface plate for sanding parts on is detrimental to its accuracy. This simple to build plate will save your surface p
From playlist Mechanics
From playlist Surface integrals
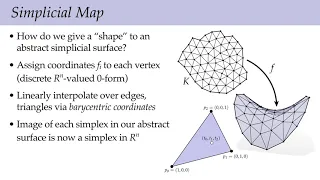
Lecture 14: Discrete Surfaces (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858

MATH331: Riemann Surfaces - part 1
We define what a Riemann Surface is. We show that PP^1 is a Riemann surface an then interpret our crazy looking conditions from a previous video about "holomorphicity at infinity" as coming from the definition of a Riemann Surface.
From playlist The Riemann Sphere

Flow through a single piece of area
From playlist Surface integrals

This video defines a cylindrical surface and explains how to graph a cylindrical surface. http://mathispower4u.yolasite.com/
From playlist Quadric, Surfaces, Cylindrical Coordinates and Spherical Coordinates

THE MAKING(English Version) (314)The Making of Steel Balls
This edition of the series of programs explaining the technology used to produce items that are familiar in our daily life features ‘Steel Balls’. A bicycle wheel spins smoothly because the wheel axle contains ball bearings. The steel balls inside the ball bearing must be close to perfectl
From playlist Engineering

Asymmetric Nose-Fairing for Wing-Body Junction by Chandan Kumar
DISCUSSION MEETING : FLUIDS DAY ORGANIZERS: Rama Govindarajan, Samriddhi Sankar Ray and Gaurav Tomar DATE : 20 January 2020 VENUE: Ramanujan Lecture Hall, ICTS Bangalore The fluid mechanics community in Bangalore has expanded enormously with different physics and engineering departments
From playlist Fluids Day 2020
Broadcasted live on Twitch -- Watch live at https://www.twitch.tv/simuleios
From playlist Misc

Fair Dice (Part 2) - Numberphile
Probability expert Professor Persi Diaconis (Stanford University) talking about dice. More links & stuff in full description below ↓↓↓ Part 1: https://youtu.be/G7zT9MljJ3Y More dice videos: http://bit.ly/Dice_Videos More Persi Diaconi videos: http://bit.ly/Persi_Videos Diaconis/Keller pa
From playlist Persi Diaconis on Numberphile

Thinking in Causation - Level 2 - Testing Causes
Thinking Slides: https://docs.google.com/presentation/d/188Hq52CBNUAOuCS5rXYMtD9tY6LPjFl1hcodejlWPJc/template/preview The Wonder of Science: https://thewonderofscience.com/mlccc22 In this video Paul Andersen shows conceptual thinking in a mini-lesson on testing causes. Two examples are
From playlist Conceptual Thinking Mini-Lessons

In How Many Ways Can an Algorithm be Fair? - Suchana Seth
Recent research in machine learning has thrown up some interesting measures of algorithmic fairness – the different ways that a predictive algorithm can be fair in its outcome. In this talk, Suchana Seth will explore what these measures of fairness imply for technology policy and regulat
From playlist Turing Seminars

Take a thorough look inside a modern jet passenger aircraft. Electronics, hydraulics, flight control surfaces, fuel system, water and waste, lighting, and more! How a Jet Engine Works: https://www.youtube.com/watch?v=L24Wf0VlTE0 CREDITS Jacob O'Neal - Modeling, animation, texturing, vfx,
From playlist Aviation - Animagraffs

Could the Loch Ness Monster be a Plesiosaur?
Today we finally finish up Loch Ness by speculating what the monster could be if I am completely wrong about it's apparent non-existence. I talk largely about plesiosaurs and leeches... so I hope you enjoy ;) All copyrighted footage and images in this video are protected under FAIR USE fo
From playlist Did dinosaurs and humans live together?

JPL and the Space Age: Sky High
Think "NASA," and what comes to mind? Astronauts? Mars rovers? Voyager and the Golden Record? How about Earth? In fact, NASA has been studying and monitoring the health of our home planet for decades, using balloons, aircraft, satellites, and even the International Space Station in the e
From playlist Earth

K-theory and actions on Euclidean retracts – Arthur Bartels – ICM2018
Topology Invited Lecture 6.8 K-theory and actions on Euclidean retracts Arthur Bartels Abstract: This note surveys axiomatic results for the Farrell–Jones Conjecture in terms of actions on Euclidean retracts and applications of these to GL_n(ℤ), relative hyperbolic groups and mapping cla
From playlist Topology

EEVblog #1047 - Solar Roadways FINALLY BUSTED! (Colas Wattway)
Dave finally puts an end to the idea of Solar Roadways. We have the test results of the world's biggest solar roadways project, the 1km long 336kW Colas Wattway project in Tourouvre France. Stand in awe at how impractical and expensive it is!, and SPOILER, how it won't usher in a new era
From playlist Solar Roadways

