
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

Polymer geometry in the large deviation regime via eigenvalue rigidity by Shirshendu Ganguly
PROGRAM :UNIVERSALITY IN RANDOM STRUCTURES: INTERFACES, MATRICES, SANDPILES ORGANIZERS :Arvind Ayyer, Riddhipratim Basu and Manjunath Krishnapur DATE & TIME :14 January 2019 to 08 February 2019 VENUE :Madhava Lecture Hall, ICTS, Bangalore The primary focus of this program will be on the
From playlist Universality in random structures: Interfaces, Matrices, Sandpiles - 2019

From playlist Contributed talks One World Symposium 2020

How do we multiply polynomials
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

Why does the distributive property Where does it come from
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

Enrique Macias-Virgo (5/27/21): Homotopic distance and Generalized motion planning
Lusternik-Schnirelmann category and topological complexity are particular cases of a more general notion, that we call homotopic distance between two maps. As a consequence, several properties of those invariants can be proved in a unified way and new results arise. For instance, we prove
From playlist Topological Complexity Seminar

Multiplying Trinomials by Binomials and Determining the Results - Math Tutorial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multilply a Binomial by a Trinomial
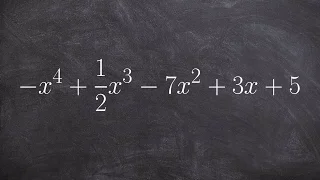
How to tell the difference between the leading coefficient and the degree of a polynomial
👉 Learn how to find the degree and the leading coefficient of a polynomial expression. The degree of a polynomial expression is the highest power (exponent) of the individual terms that make up the polynomial. For terms with more that one variable, the power (exponent) of the term is the s
From playlist Find the leading coefficient and degree of a polynomial | expression

Nexus Trimester - Mokshay Madiman (University of Delaware)
The Stam region, or the differential entropy region for sums of independent random vectors Mokshay Madiman (University of Delaware) February 25, 2016 Abstract: Define the Stam region as the subset of the positive orthant in [Math Processing Error] that arises from considering entropy powe
From playlist Nexus Trimester - 2016 - Fundamental Inequalities and Lower Bounds Theme
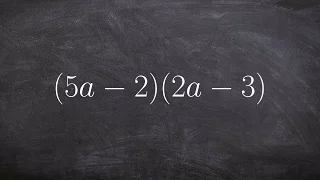
Using foil to Multiply Two Binomials - Math Tutorial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials
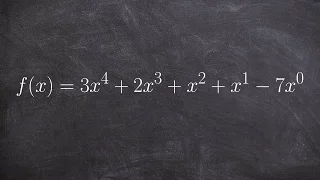
What is the definition of standard form, degree and leading coefficient of a polynomial
👉 Learn how to find the degree and the leading coefficient of a polynomial expression. The degree of a polynomial expression is the the highest power (exponent) of the individual terms that make up the polynomial. For terms with more that one variable, the power (exponent) of the term is t
From playlist Find the leading coefficient and degree of a polynomial | equation

How to Multiply to Binomials Using Distributive Property - Polynomial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

Using the Box Method to Multiply Two Binomials - Math Tutorial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

Entanglement entropy, quantum field theory, and holography by Matthew Headrick
26 December 2016 to 07 January 2017 VENUE : Madhava Lecture Hall, ICTS, Bengaluru Information theory and computational complexity have emerged as central concepts in the study of biological and physical systems, in both the classical and quantum realm. The low-energy landscape of classic
From playlist US-India Advanced Studies Institute: Classical and Quantum Information
