
Sum of integers squared explained
Explanation on deriving the equation. In arithmetic, we often come across the sum of n natural numbers. Sum of squares refers to the sum of the squares of numbers. It is basically the addition of squared numbers. Support my channel with this special custom merch! https://www.etsy.com/list
From playlist Math formulas, proofs, ideas explained
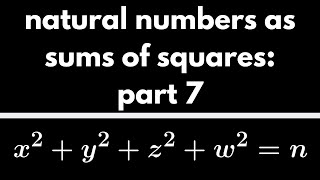
Number Theory | Sums of Squares Part 7.
Our final video in this series where we have examined which natural numbers are expressible as a sum of various numbers of square integers. Here we show that all natural numbers are expressible as a sum of four squares. http://www.michael-penn.net http://www.randolphcollege.edu/mathematic
From playlist Sums of Squares
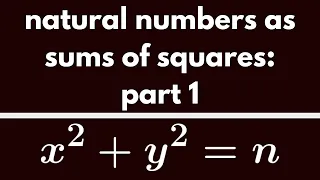
Number Theory | Sums of Squares Part 1.
This is the first in a series of videos where we establish which natural numbers are expressible as the sum of two squares. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Sums of Squares

Algebra to remember when evaluating sum and difference formulas
👉 Learn how to simplify trigonometric function of the sum or difference of two angles using the sum/difference formulas. To do this, we first use the unit circle and Pythagoras theorem to identify and obtain the values of the needed trigonometric functions of the known angles. When we know
From playlist Sum and Difference Formulas
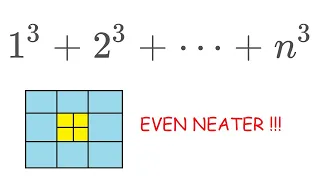
In this video, I give an explicit formula for the sum of cubes, and I show in particular why it’s the square of the sum of integers. It is really clever and neat, enjoy! Sum of squares: https://youtu.be/gVMEtOXdhs8 Subscribe to my channel: https://youtu.be/c/drpeyam
From playlist Cool proofs

Function Arithmetic (Sum): (f+g)(x) and (f+g)(4) - Quadratic
This video explains how to determine the sum of two quadratic functions. Then a function value is determined using two methods. http://mathispower4u.com
From playlist The Properties of Functions

Number Theory | Sums of Squares Part 4
We provide a few examples of writing natural numbers as sums of two squares. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Sums of Squares
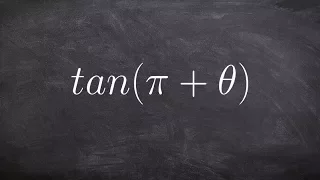
Simplifying a trigonometric expression using tangent
👉 Learn how to simplify trigonometric function of the sum or difference of two angles using the sum/difference formulas. To do this, we first use the unit circle and Pythagoras theorem to identify and obtain the values of the needed trigonometric functions of the known angles. When we know
From playlist Sum and Difference Formulas
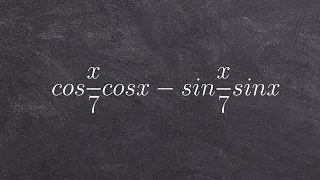
Write an expression as a single trigonometric function using sum and difference formula
👉 Learn how to write a given sum or difference of two angles formula expression as a single sum/difference of angles trigonometric function. To do this, we first identify the trigonometric function for which its sum/difference formula is given and identify the individual angles. Then we ca
From playlist Sum and Difference Formulas

CTNT 2020 - Sieves (by Brandon Alberts) - Lecture 2
The Connecticut Summer School in Number Theory (CTNT) is a summer school in number theory for advanced undergraduate and beginning graduate students, to be followed by a research conference. For more information and resources please visit: https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2020 - Sieves (by Brandon Alberts)

The Basel Problem Part 2: Euler's Proof and the Riemann Hypothesis
In this video, I present Euler's proof that the solution to the Basel problem is pi^2/6. I discuss a surprising connection Euler discovered between a generalization of the Basel problem and the Bernoulli numbers, as well as his invention of the zeta function. I explain Euler's discovery of
From playlist Analytic Number Theory

Alexandra Florea: The Ratios Conjecture over function fields
I will talk about some recent joint work with H. Bui and J. Keating where we study the Ratios Conjecture for the family of quadratic L-functions over function fields. I will also discuss the closely related problem of obtaining upper bounds for negative moments of L-functions, which allows
From playlist Seminar Series "Arithmetic Applications of Fourier Analysis"

Moments of large families of Dirichlet L-functions - Vorrapan Chandee
50 Years of Number Theory and Random Matrix Theory Conference Topic: Moments of large families of Dirichlet L-functions Speaker: Vorrapan Chandee Affiliation: Kansas State University Date: June 24, 2022 Sixth and higher moments of L-functions are important and challenging problems in ana
From playlist Mathematics

Quadratic Twists of Modular L-Functions - Xiannan Li
Joint IAS/PU Number Theory Seminar Topic: Quadratic Twists of Modular L-Functions Speaker: Xiannan Li Affiliation: Kansas State University Date: December 08, 2022 The behavior of quadratic twists of modular L-functions is at the critical point is related both to coefficients of half int
From playlist Mathematics

Introduction to Probability and Statistics 131A. Lecture 9. Conditional Probability
UCI Math 131A: Introduction to Probability and Statistics (Summer 2013) Lec 09. Introduction to Probability and Statistics: Conditional Probability View the complete course: http://ocw.uci.edu/courses/math_131a_introduction_to_probability_and_statistics.html Instructor: Michael C. Cransto
From playlist Math 131A: Introduction to Probability and Statistics

Euler's harmonic number identity.
We prove a special case of Euler's harmonic number identity. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Mathematics named after Leonhard Euler

Some identities involving the Riemann-Zeta function.
After introducing the Riemann-Zeta function we derive a generating function for its values at positive even integers. This generating function is used to prove two sum identities. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function

1 + 2 + 3 + 4 + 5 + 6 + ... = –1/12 | Six proofs | Divergent Series
This video presents six proofs of the famous sum of the monotonic divergent series of natural numbers 1 + 2 + 3 + 4 + 5 + 6 + ... = –1/12 00:00 Introduction 00:15 Proof 1 – Generating Function 03:49 Proof 2 – Direct Calculation 06:50 Proof 3 – Intercept Function 11:13 Proof 4 – Partia
From playlist Summer of Math Exposition 2 videos

What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics

How to find the exact value by using the sum of two angles formula with tangent
👉 Learn how to evaluate the tangent of an angle in degrees using the sum/difference formulas. To do this, we first express the given angle as a sum or a difference of two (easy to evaluate) angles, then we use the unit circle and the Pythagoras theorem to identify the angles and obtain all
From playlist Sum and Difference Formulas