
Linear Algebra: Continuing with function properties of linear transformations, we recall the definition of an onto function and give a rule for onto linear transformations.
From playlist MathDoctorBob: Linear Algebra I: From Linear Equations to Eigenspaces | CosmoLearning.org Mathematics

2 Construction of a Matrix-YouTube sharing.mov
This video shows you how a matrix is constructed from a set of linear equations. It helps you understand where the various elements in a matrix comes from.
From playlist Linear Algebra

Group Definition (expanded) - Abstract Algebra
The group is the most fundamental object you will study in abstract algebra. Groups generalize a wide variety of mathematical sets: the integers, symmetries of shapes, modular arithmetic, NxM matrices, and much more. After learning about groups in detail, you will then be ready to contin
From playlist Abstract Algebra
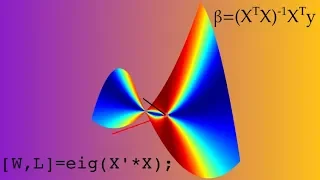
This is part of an online course on beginner/intermediate linear algebra, which presents theory and implementation in MATLAB and Python. The course is designed for people interested in applying linear algebra to applications in multivariate signal processing, statistics, and data science.
From playlist Linear algebra: theory and implementation

Linear Algebra Proofs 11d: Left Inverse Is Right Inverse - A and A^-1 Commute
This course is on Lemma: http://lem.ma Lemma looking for developers: http://lem.ma/jobs Other than http://lem.ma, I recommend Strang http://bit.ly/StrangYT, Gelfand http://bit.ly/GelfandYT, and my short book of essays http://bit.ly/HALAYT Questions and comments below will be prompt
From playlist Linear Algebra Proofs

What is Abstract Algebra? (Modern Algebra)
Abstract Algebra is very different than the algebra most people study in high school. This math subject focuses on abstract structures with names like groups, rings, fields and modules. These structures have applications in many areas of mathematics, and are being used more and more in t
From playlist Abstract Algebra

Linear Algebra Vignette 2a: RREF - What It's For
This course is on Lemma: http://lem.ma Lemma looking for developers: http://lem.ma/jobs Other than http://lem.ma, I recommend Strang http://bit.ly/StrangYT, Gelfand http://bit.ly/GelfandYT, and my short book of essays http://bit.ly/HALAYT Questions and comments below will be prompt
From playlist Linear Algebra Vignettes

Linear Algebra Full Course for Beginners to Experts
Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as lines, planes and rotations. Also, functional analysis may be basically viewed as the application of l
From playlist Linear Algebra

Go Lesson 9: Opening Play with the 4_4 point and low approach move | Playing Go | N J Wildberger
Perhaps the most popular opening move these days (the bots love it), is the 4-4 point. In this video we look at some opening sequences involving a low approach move by the opponent. A lot of patterns here are relatively simple and easy to understand -- and they certainly will crop up a lo
From playlist Playing Go

Linear Algebra Vignette 3d: Easy Eigenvalues - Linearly Dependent Columns
This course is on Lemma: http://lem.ma Lemma looking for developers: http://lem.ma/jobs Other than http://lem.ma, I recommend Strang http://bit.ly/StrangYT, Gelfand http://bit.ly/GelfandYT, and my short book of essays http://bit.ly/HALAYT Questions and comments below will be prompt
From playlist Linear Algebra Vignettes

Lara Ismert: "Heisenberg Pairs on Hilbert C*-modules"
Actions of Tensor Categories on C*-algebras 2021 "Heisenberg Pairs on Hilbert C*-modules" Lara Ismert - Embry-Riddle Aeronautical University, Mathematics Abstract: Roughly speaking, a Heisenberg pair on a Hilbert space is a pair of self-adjoint operators (A,B) which satisfy the Heisenber
From playlist Actions of Tensor Categories on C*-algebras 2021

Go Lesson 8: Opening play with the 3_4 point and low approach move | Playing Go | N J Wildberger
When learning how to play Go, some basic familiarity with common opening patterns, called Joseki in Japanese, is essential. These are typically centred around the corner. In this video we look at what is historically perhaps the most common and thoroughly studied situation: where a play at
From playlist Playing Go

Go lesson 12: Basic fighting skills after a corner attachment | Playing Go | N J Wildberger
In this video on Playing Go, we analyse some basic positions around the corner that lead to some direct fighting. We meet several useful patterns and tactics that are important for beginners to see. This is part of a sequence of introductory lessons in how to play Go. The entire playl
From playlist Playing Go

CU Boulder 2020 Mathematics Virtual Graduation Ceremony
Congratulations to the Mathematics Class of 2020
From playlist My Students

Go Lesson 7: Opening play with the 3_4 point | Playing Go | N J Wildberger
We continue our survey of important joseki, or opening patterns, for beginners learning to play the game of Go. Here we consider the 3_4 point, which leads to hundreds of established plays, but we choose some simple ones where the opponent plays a high approach move. These patterns also t
From playlist Playing Go

Go Lesson 13: Honinbo Sansa VS Rigen (~1600) | Playing Go | N J Wildberger
A classic game from Imperial Japan -- the Shogun era, between two prominent players, Honinbo Sansa versus Rigen. The game was played sometime in the 1600's. It features quite fierce fighting between rival groups trying to surround and kill each other. Despite both players being seemingly o
From playlist Playing Go

Go Lesson 5: A game played to the end | Playing Go | N J Wildberger
Let's have a look at a very peaceful game between your protagonist and the clever bot DCNN1d01 (4D). I want to show you how a game ends and how the final score is counted. And you will have a chance to see some reasonable flow of moves, not particularly sharp, but rather slow and steady on
From playlist Playing Go

Guoliang Yu: Dimension, complexity and K theory
The lecture was held within the framework of Follow-up Workshop TP Rigidity. 29.4.2015
From playlist HIM Lectures 2015

Linear Algebra Vignette 1a: Matrix Representation of a Linear Transformation
This course is on Lemma: http://lem.ma Lemma looking for developers: http://lem.ma/jobs Other than http://lem.ma, I recommend Strang http://bit.ly/StrangYT, Gelfand http://bit.ly/GelfandYT, and my short book of essays http://bit.ly/HALAYT Questions and comments below will be prompt
From playlist Linear Algebra Vignettes

Markus Haase : Operators in ergodic theory - Lecture 1 : Operators dynamics versus ...
Abstract : The titles of the of the individual lectures are: 1. Operators dynamics versus base space dynamics 2. Dilations and joinings 3. Compact semigroups and splitting theorems Recording during the thematic meeting : "Probabilistic Aspects of Multiple Ergodic Averages " the December 6
From playlist Jean-Morlet Chair - Lemanczyk/Ferenczi