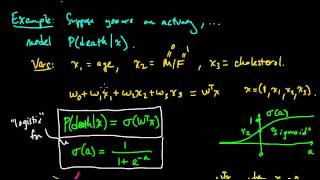(ML 19.1) Gaussian processes - definition and first examples
Definition of a Gaussian process. Elementary examples of Gaussian processes.
From playlist Machine Learning

Dihedral Group (Abstract Algebra)
The Dihedral Group is a classic finite group from abstract algebra. It is a non abelian groups (non commutative), and it is the group of symmetries of a regular polygon. This group is easy to work with computationally, and provides a great example of one connection between groups and geo
From playlist Abstract Algebra
If you are interested in learning more about this topic, please visit http://www.gcflearnfree.org/ to view the entire tutorial on our website. It includes instructional text, informational graphics, examples, and even interactives for you to practice and apply what you've learned.
From playlist Machine Learning

Group Definition (expanded) - Abstract Algebra
The group is the most fundamental object you will study in abstract algebra. Groups generalize a wide variety of mathematical sets: the integers, symmetries of shapes, modular arithmetic, NxM matrices, and much more. After learning about groups in detail, you will then be ready to contin
From playlist Abstract Algebra

(PP 6.1) Multivariate Gaussian - definition
Introduction to the multivariate Gaussian (or multivariate Normal) distribution.
From playlist Probability Theory

(ML 19.2) Existence of Gaussian processes
Statement of the theorem on existence of Gaussian processes, and an explanation of what it is saying.
From playlist Machine Learning

(PP 6.3) Gaussian coordinates does not imply (multivariate) Gaussian
An example illustrating the fact that a vector of Gaussian random variables is not necessarily (multivariate) Gaussian.
From playlist Probability Theory

Symmetric Groups (Abstract Algebra)
Symmetric groups are some of the most essential types of finite groups. A symmetric group is the group of permutations on a set. The group of permutations on a set of n-elements is denoted S_n. Symmetric groups capture the history of abstract algebra, provide a wide range of examples in
From playlist Abstract Algebra

Jacob explains the fundamental concepts in group theory of what groups and subgroups are, and highlights a few examples of groups you may already know. Abelian groups are named in honor of Niels Henrik Abel (https://en.wikipedia.org/wiki/Niels_Henrik_Abel), who pioneered the subject of
From playlist Basics: Group Theory