
C49 Example problem solving a system of linear DEs Part 1
Solving an example problem of a system of linear differential equations, where one of the equations is not homogeneous. It's a long problem, so this is only part 1.
From playlist Differential Equations

Separable Differential Equations (Differential Equations 12)
https://www.patreon.com/ProfessorLeonard How to solve Separable Differential Equations by Separation of Variables. Lots of examples!!
From playlist Differential Equations

Stable Homotopy Seminar, 18: The Steenrod Algebra (Liam Keenan)
Liam defines the Steenrod algebra, as the endomorphisms of the Eilenberg-MacLane spectrum HF_p. This naturally acts on the mod p cohomology of any space (or spectrum), and we look at the example of the mod 2 cohomology of RP^infinity. He states some of its fundamental properties allowing u
From playlist Stable Homotopy Seminar

C19 Example problem using the superposition principle
Example problem using the superposition approach.
From playlist Differential Equations

CU Boulder 2020 Mathematics Virtual Graduation Ceremony
Congratulations to the Mathematics Class of 2020
From playlist My Students

C20 Example problem using the superposition principle
Another example problem.
From playlist Differential Equations
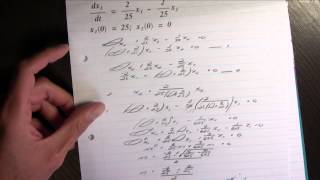
C51 Example problem of a system of linear DEs
Example problem solving a system of linear differential equations.
From playlist Differential Equations

C50 Example problem solving a system of linear DEs Part 2
Part 2 of the prvious example problem, solving a system of linear differential equations, where one of the equations is non-homogeneous.
From playlist Differential Equations

Homological Algebra(Homo Alg) 4 by Graham Ellis
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

Graphing the system of two linear inequalities with two horizontal line
👉 Learn how to graph a system of inequalities. A system of inequalities is a set of inequalities which are collectively satisfied by a certain range of values for the variables. To graph a system of inequalities, each inequality making up the system is graphed individually with the side of
From playlist Solve a System of Inequalities by Graphing

Separable differential equation example
Learn how to solve a separable differential equation. To learn how to solve different types of differential equations: Check out the differential equation playlist: 👉 https://bit.ly/bprpdiffeq Check out my Diff Eq Ultimate Study Guide: 👉 https://youtu.be/e-cTygNbEUE For more calculus &
From playlist Differential Equations: Separable (Nagle Sect2.2)

Stable Homotopy Seminar, 20: Computations with the Adams Spectral Sequence (Jacob Hegna)
Jacob Hegna walks us through some of the methods which have been used to compute the E_2 page of the Adams spectral sequence for the sphere, a.k.a. Ext_A(F_2, F_2), where A is the Steenrod algebra. The May spectral sequence works by filtering A and first computing Ext over the associated g
From playlist Stable Homotopy Seminar

Problem #24 Circuit with Five Resistors
Problem #24 Circuit with Five Resistors
From playlist Bi-weekly Physics Problems

Introduction to Fiber Bundles part 1: Definitions
We give the definition of a fiber bundle with fiber F, trivializations and transition maps. This is a really basic stuff that we use a lot. Here are the topics this sets up: *Associated Bundles/Principal Bundles *Reductions of Structure Groups *Steenrod's Theorem *Torsor structure on arith
From playlist Fiber bundles

Stable Homotopy Seminar, 21: Computing Homotopy Groups with the Adams Spectral Sequence (Zach Himes)
Zachary Himes constructs the May spectral sequence, a tool using a filtration of of the dual Steenrod algebra that calculates the E2 page of the Adams spectral sequence. May's original insight was that the associated graded of the dual Steenrod algebra is a primitively generated Hopf algeb
From playlist Stable Homotopy Seminar

Sergey Melikhov, Steklov Math Institute (Moscow) Title: Fine Shape Abstract: A shape theory is something which is supposed to agree with homotopy theory on polyhedra and to treat more general spaces by looking at their polyhedral approximations. Or if you prefer, it is something which is s
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

Jeremy Dubut: Natural homology computability and Eilenberg Steenrod axioms
The lecture was held within the framework of the Hausdorff Trimester Program : Applied and Computational Algebraic Topology
From playlist HIM Lectures: Special Program "Applied and Computational Algebraic Topology"

Introduction to Fiber Bundles Part 5.1: Steenrod's Theorem
This video is about how to reduce structure groups of fiber bundles.
From playlist Fiber bundles

Anibal Medina, "Persistence Steenrod modules"
The talk is part of the Workshop Topology of Data in Rome (15-16/09/2022) https://www.mat.uniroma2.it/Eventi/2022/Topoldata/topoldata.php The event was organized in partnership with the Romads Center for Data Science https://www.mat.uniroma2.it/~rds/about.php The Workshop was hosted and
From playlist Workshop: Topology of Data in Rome
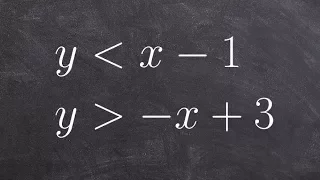
Graphing a system of two inequalities in slope intercept form
👉 Learn how to graph a system of inequalities. A system of inequalities is a set of inequalities which are collectively satisfied by a certain range of values for the variables. To graph a system of inequalities, each inequality making up the system is graphed individually with the side of
From playlist Solve a System of Inequalities by Graphing