Stability radius
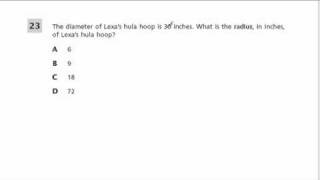
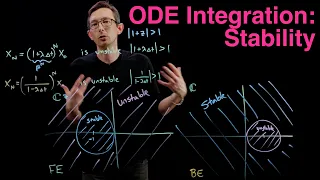
In mathematics, the stability radius of an object (system, function, matrix, parameter) at a given nominal point is the radius of the largest ball, centered at the nominal point, all of whose elements satisfy pre-determined stability conditions. The picture of this intuitive notion is this: where denotes the nominal point, denotes the space of all possible values of the object , and the shaded area, , represents the set of points that satisfy the stability conditions. The radius of the blue circle, shown in red, is the stability radius. (Wikipedia).