Spherical segment
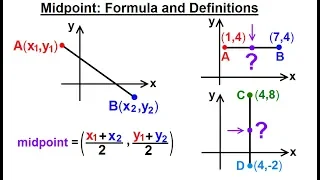
In geometry, a spherical segment is the solid defined by cutting a sphere or a ball with a pair of parallel planes.It can be thought of as a spherical cap with the top truncated, and so it corresponds to a spherical frustum. The surface of the spherical segment (excluding the bases) is called spherical zone. If the radius of the sphere is called R, the radii of the spherical segment bases are r1 and r2, and the height of the segment (the distance from one parallel plane to the other) called h, then the volume of the spherical segment is The curved surface area of the spherical zone—which excludes the top and bottom bases—is given by (Wikipedia).