
Jean Michel : Quasisemisimple classes
Abstract: This is a report on joint work with François Digne. Quasisemisimple elements are a generalisation of semisimple elements to disconnected reductive groups (or equivalently, to algebraic automorphisms of reductive groups). In the setting of reductive groups over an algebraically c
From playlist Lie Theory and Generalizations

Groups in abstract algebra examples
In this tutorial I discuss two more examples of groups. The first contains four elements and they are the four fourth roots of 1. The second contains only three elements and they are the three cube roots of 1. Under the binary operation of multiplication, these sets are in fact groups.
From playlist Abstract algebra
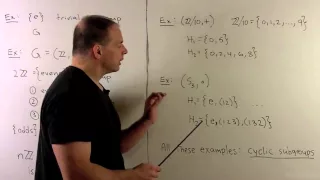
Abstract Algebra: We define the notion of a subgroup and provide various examples. We also consider cyclic subgroups and subgroups generated by subsets in a given group G. Example include A4 and D8. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-
From playlist Abstract Algebra

Bachir Bekka - On characters of infinite groups
Let G be a countable infinite group. Unless G is virtually abelian, a description of the unitary dual of G (that is, the equivalence classes of irreducible unitary representations of G) is hopeless, as a consequence of theorems of Glimm and Thoma. A sensible substitute for the unitary dual
From playlist Groupes, géométrie et analyse : conférence en l'honneur des 60 ans d'Alain Valette

Constructing group actions on quasi-trees – Koji Fujiwara – ICM2018
Topology Invited Lecture 6.12 Constructing group actions on quasi-trees Koji Fujiwara Abstract: A quasi-tree is a geodesic metric space quasi-isometric to a tree. We give a general construction of many actions of groups on quasi-trees. The groups we can handle include non-elementary hype
From playlist Topology

In this tutorial we define a subgroup and prove two theorem that help us identify a subgroup. These proofs are simple to understand. There are also two examples of subgroups.
From playlist Abstract algebra

Simple Groups - Abstract Algebra
Simple groups are the building blocks of finite groups. After decades of hard work, mathematicians have finally classified all finite simple groups. Today we talk about why simple groups are so important, and then cover the four main classes of simple groups: cyclic groups of prime order
From playlist Abstract Algebra
Advice to Amateur Research Mathematicians: Poly Number theory-- future directions for greater import
Number theory is a very attractive subject, but in this video we argue that for prospective amateur researchers, the chance of making an important contribution is minimal. Better to focus on a much bigger and more wide open area: Poly Number theory! Polynumbers, developed in the Algebrai
From playlist Maxel inverses and orthogonal polynomials (non-Members)

Numerical mathematics of quasicrystals – Pingwen Zhang – ICM2018
Numerical Analysis and Scientific Computing Invited Lecture 15.8 Numerical mathematics of quasicrystals Pingwen Zhang Abstract: Quasicrystals are one kind of fascinating aperiodic structures, and give a strong impact on material science, solid state chemistry, condensed matter physics an
From playlist Numerical Analysis and Scientific Computing

Rainbow structures, Latin squares & graph decompositions - Benny Sudakov
Computer Science/Discrete Mathematics Seminar I Topic: Rainbow structures, Latin squares & graph decompositions Speaker: Benny Sudakov Affiliation: ETH Zürich Date: March 01, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

Also known as Graeco-Latin Squares. Featuring Dr James Grime. Extra footage at: https://youtu.be/HuIrUeODtVQ Patreon: http://www.patreon.com/numberphile More links & stuff in full description below ↓↓↓ Dr James Grime's website: https://www.singingbanana.com More James Grime videos on Num
From playlist James Grime on Numberphile
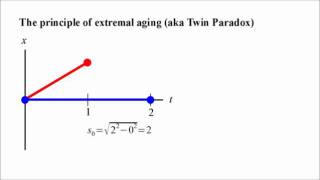
Relativity 8 - the yardstick of spacetime
The final piece of the puzzle falls in place. Herman Minkowski showed that Special Relativity defines a spacetime invariant - the "proper time" - between two events. Einstein's insight into the equivalence between falling and floating allowed him to realize that this also applied to Genera
From playlist Relativity

R - Grammar Analysis with Logistic Regression
Lecturer: Dr. Erin M. Buchanan Summer 2019 https://www.patreon.com/statisticsofdoom This video is part of my human language modeling class. This video continues with co-relations by using distinctive collexeme analysis to determine the likelihood of collocates (combinations of words). N
From playlist Human Language (ANLY 540)

LA Rubyconf 2015- Stupid Ideas For Many Computers by Aja Hammerly
Stupid Ideas For Many Computers There are plenty of useful things you can do with Ruby and a bunch of servers. This talk isn't about useful things. This talk will show off asinine, amusing, and useless things you can do with Ruby and access to cloud computing. Sentiment analysis based on
From playlist LA Rubyconf 2015

RubyConf 2015 - Keynote: Stupid Ideas for Many Computers by Aja Hammerly
Keynote: Stupid Ideas for Many Computers by Aja Hammerly There are plenty of useful things you can do with Ruby and a bunch of servers. This talk isn't about useful things. This talk will show off asinine, amusing, and useless things you can do with Ruby and access to cloud computing. Se
From playlist RubyConf 2015

Asymptotic enumeration of graphs with given degree sequence – Nicholas Wormald – ICM2018
Combinatorics Invited Lecture 13.7 Asymptotic enumeration of graphs with given degree sequence Nicholas Wormald Abstract: We survey results on counting graphs with given degree sequence, focusing on asymptotic results, and mentioning some of the applications of these results. The main re
From playlist Combinatorics

Some thoughts on Gaussian processes for emulation of deterministic computer models: Michael Stein
Uncertainty quantification (UQ) employs theoretical, numerical and computational tools to characterise uncertainty. It is increasingly becoming a relevant tool to gain a better understanding of physical systems and to make better decisions under uncertainty. Realistic physical systems are
From playlist Effective and efficient gaussian processes

Art Historian Dr. Vida Hull ETSU Online Programs - http://www.etsu.edu/online Italian Renaissance Art History Survey II 13 Bramante 4th ed
From playlist ETSU: ARTH 4037 Italian Renaissance | CosmoLearning.org Art

Center of a group in abstract algebra
After the previous video where we saw that two of the elements in the dihedral group in six elements commute with all the elements in the group, we finally get to define the center of a group. The center of a group is a subgroup and in this video we also go through the proof to show this.
From playlist Abstract algebra

Hypergraph matchings and designs – Peter Keevash – ICM2018
Combinatorics Invited Lecture 13.10 Hypergraph matchings and designs Peter Keevash Abstract: We survey some aspects of the perfect matching problem in hypergraphs, with particular emphasis on structural characterisation of the existence problem in dense hypergraphs and the existence of d
From playlist Combinatorics