
Introduction to ADVANCED CALCULUS Sets and Notation
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Introduction to ADVANCED CALCULUS Sets and Notation - Definition of a Set and notion/symbols denoting set membership. - Set builder and interval notation. - Definition of union and intersection of sets and set complement. - The set
From playlist Advanced Calculus

Math 131 Lecture #04 091216 Complex Numbers, Countable and Uncountable Sets
Recall the complex numbers: the plane with addition and multiplication. Geometric interpretation of operations. Same thing as a+bi. Complex conjugate. Absolute value (modulus) of a complex numbers; properties (esp., triangle inequality). Cauchy-Schwarz inequality. Recall Euclidean sp
From playlist Course 7: (Rudin's) Principles of Mathematical Analysis

Number Theory - Fundamental Theorem of Arithmetic
Fundamental Theorem of Arithmetic and Proof. Building Block of further mathematics. Very important theorem in number theory and mathematics.
From playlist Proofs

In this video, Tori explains the meaning of a set. She looks into finite versus infinite sets, and explains elements.
From playlist Basics: College Algebra

Calculus - The Fundamental Theorem, Part 1
The Fundamental Theorem of Calculus. First video in a short series on the topic. The theorem is stated and two simple examples are worked.
From playlist Calculus - The Fundamental Theorem of Calculus

Calculus - The Fundamental Theorem, Part 3
The Fundamental Theorem of Calculus. Specific examples of simple functions, and how the antiderivative of these functions relates to the area under the graph.
From playlist Calculus - The Fundamental Theorem of Calculus

This lecture is on Introduction to Higher Mathematics (Proofs). For more see http://calculus123.com.
From playlist Proofs

What is the Fundamental theorem of Algebra, really? | Abstract Algebra Math Foundations 217
Here we give restatements of the Fundamental theorems of Algebra (I) and (II) that we critiqued in our last video, so that they are now at least meaningful and correct statements, at least to the best of our knowledge. The key is to abstain from any prior assumptions about our understandin
From playlist Math Foundations

Nigel Higson: The Oka principle and Novodvorskii’s theorem
Talk by Jonathan Rosenberg in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-Seminar.html on November 11, 2020.
From playlist Global Noncommutative Geometry Seminar (Americas)

The affine Hecke category is a monoidal colimit - James Tao
Geometric and Modular Representation Theory Seminar Topic: The affine Hecke category is a monoidal colimit Speaker: James Tao Affiliation: Massachusetts Institute of Technology Date: February 24, 2021 For more video please visit http://video.ias.edu
From playlist Seminar on Geometric and Modular Representation Theory

Representation theory and geometry – Geordie Williamson – ICM2018
Plenary Lecture 17 Representation theory and geometry Geordie Williamson Abstract: One of the most fundamental questions in representation theory asks for a description of the simple representations. I will give an introduction to this problem with an emphasis on the representation theor
From playlist Plenary Lectures

8ECM Invited Lecture: Stuart White
From playlist 8ECM Invited Lectures

Christopher Schafhauser: On the classification of nuclear simple C*-algebras, Lecture 3
Mini course of the conference YMC*A, August 2021, University of Münster. Abstract: A conjecture of George Elliott dating back to the early 1990’s asks if separable, simple, nuclear C*-algebras are determined up to isomorphism by their K-theoretic and tracial data. Restricting to purely i
From playlist YMC*A 2021

2 - Kick-off afternoon : Georges Gonthier, Digitizing the Group Theory of the Odd Order Theorem
Georges Gonthier (Microsoft Research, Cambridge, and Microsoft INRIA Joint Center, Palaiseau): Digitizing the Group Theory of the Odd Order Theorem
From playlist T2-2014 : Semantics of proofs and certified mathematics
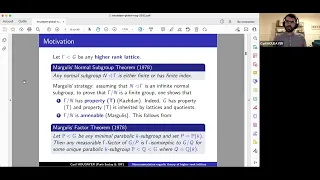
Cyril Houdayer: Noncommutative ergodic theory of lattices in higher rank simple algebraic groups
Talk by Cyril Houdayer in the Global Noncommutative Geometry Seminar (Americas) on March 18, 2022. https://globalncgseminar.org/talks/tba-28/
From playlist Global Noncommutative Geometry Seminar (Americas)

Locally Potentially Equivalent Galois Representations by C S Rajan
PROGRAM ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (HYBRID) ORGANIZERS: Ashay Burungale (CalTech/UT Austin, USA), Haruzo Hida (UCLA), Somnath Jha (IIT Kanpur) and Ye Tian (MCM, CAS) DATE: 08 August 2022 to 19 August 2022 VENUE: Ramanujan Lecture Hall and online The program pla
From playlist ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (2022)

From continuous rational to regulous functions – Krzysztof Kurdyka & Wojciech Kucharz – ICM2018
Algebraic and Complex Geometry Invited Lecture 4.6 From continuous rational to regulous functions Krzysztof Kurdyka & Wojciech Kucharz Abstract: Let X be an algebraic set in ℝⁿ. Real-valued functions, defined on subsets of X, that are continuous and admit a rational representation have s
From playlist Algebraic & Complex Geometry

From playlist Abstract Algebra 1

Hodge Theory, between Algebraicity and Transcendence (Lecture 5) by Bruno Klingler
DISCUSSION MEETING TOPICS IN HODGE THEORY (HYBRID) ORGANIZERS: Indranil Biswas (TIFR, Mumbai, India) and Mahan Mj (TIFR, Mumbai, India) DATE: 20 February 2023 to 25 February 2023 VENUE: Ramanujan Lecture Hall and Online This is a followup discussion meeting on complex and algebraic ge
From playlist Topics in Hodge Theory - 2023
