
Introduction to Homotopy Theory- PART 1: UNIVERSAL CONSTRUCTIONS
The goal of this series is to develop homotopy theory from a categorical perspective, alongside the theory of model categories. We do this with the hope of eventually developing stable homotopy theory, a personal goal a passion of mine. I'm going to follow nLab's notes, but I hope to add t
From playlist Introduction to Homotopy Theory

Introduction to Homotopy Theory- Part 5- Transition to Abstract Homotopy Theory
Credits: nLab: https://ncatlab.org/nlab/show/Introdu... Animation library: https://github.com/3b1b/manim Music: ► Artist Attribution • Music By: "KaizanBlu" • Track Name: "Remember (Extended Mix)" • YouTube Track Link: https://bit.ly/31Ma5s0 • Spotify Track Link: https://spoti.fi/
From playlist Introduction to Homotopy Theory

Homotopy Group - (1)Dan Licata, (2)Guillaume Brunerie, (3)Peter Lumsdaine
(1)Carnegie Mellon Univ.; Member, School of Math, (2)School of Math., IAS, (3)Dalhousie Univ.; Member, School of Math April 11, 2013 In this general survey talk, we will describe an approach to doing homotopy theory within Univalent Foundations. Whereas classical homotopy theory may be des
From playlist Mathematics

Homotopy type theory: working invariantly in homotopy theory -Guillaume Brunerie
Short talks by postdoctoral members Topic: Homotopy type theory: working invariantly in homotopy theory Speaker: Guillaume Brunerie Affiliation: Member, School of Mathematics Date: September 26, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Lie Groups and Lie Algebras: Lesson 34 -Introduction to Homotopy
Lie Groups and Lie Algebras: Introduction to Homotopy In order to proceed with Gilmore's study of Lie groups and Lie algebras we now need a concept from algebraic topology. That concept is the notion of homotopy and the Fundamental Group of a topological space. In this lecture we provide
From playlist Lie Groups and Lie Algebras

Homomorphisms in abstract algebra
In this video we add some more definition to our toolbox before we go any further in our study into group theory and abstract algebra. The definition at hand is the homomorphism. A homomorphism is a function that maps the elements for one group to another whilst maintaining their structu
From playlist Abstract algebra

ITHT: Part 12- Model Structure on Topological Spaces
Credits: nLab: https://ncatlab.org/nlab/show/Introduction+to+Homotopy+Theory#TheClassicalModelStructureOfTopologicalSpaces Animation library: https://github.com/3b1b/manim My own code/modified library: https://github.com/treemcgee42/youtub...
From playlist Introduction to Homotopy Theory

Christoph Winges: On the isomorphism conjecture for Waldhausen's algebraic K-theory of spaces
The lecture was held within the framework of the (Junior) Hausdorff Trimester Program Topology: "The Farrell-Jones conjecture" I will survey recent progress on the isomorphism conjecture for Waldhausen's "algebraic K-theory of spaces" functor, and how this relates to the original isomorp
From playlist HIM Lectures: Junior Trimester Program "Topology"

Christoph Winges: Automorphisms of manifolds and the Farrell Jones conjectures
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Building on previous work of Bartels, Lück, Reich and others studying the algebraic K-theory and L-theory of discrete group rings, the validity of the Farrell-Jones Conjecture has be
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

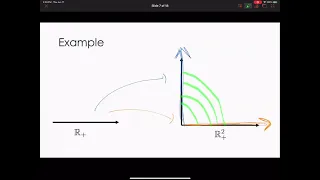
Introduction to Homotopy Theory- PART 2: (TOPOLOGICAL) HOMOTOPY
We move on to the second section of nLab's introduction to homotopy theory, homotopy. Topics covered include left/right homotopy, topolocial path/cylinder objects, homotopy groups, and weak/standard homotopy equivalences. PLEASE leave any misconceptions I had or inaccuracies in my video i
From playlist Introduction to Homotopy Theory

Algebraic Topology - 11.3 - Homotopy Equivalence
We sketch why that the homotopy category is a category.
From playlist Algebraic Topology

Michael Hopkins: Bernoulli numbers, homotopy groups, and Milnor
Abstract: In his address at the 1958 International Congress of Mathematicians Milnor described his joint work with Kervaire, relating Bernoulli numbers, homotopy groups, and the theory of manifolds. These ideas soon led them to one of the most remarkable formulas in mathematics, relating f
From playlist Abel Lectures

Erin Wolf Chambers (5/12/22): Computing optimal homotopies
The question of how to measure similarity between curves in various settings has received much attention recently, motivated by applications in GIS data analysis, medical imaging, and computer graphics. Geometric measures such as Hausdorff and Fr\'echet distance have efficient algorithms,
From playlist Bridging Applied and Quantitative Topology 2022

Duality In Higher Categories II by Pranav Pandit
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)

Wojciech Chachólski (4/29/20): TDA invariants and model categories
Title: TDA invariants and model categories Abstract: Data analysis is a balancing act of simplification and ignoring most of the information available on the one hand, and retaining what might be meaningful for the particular task on the other. The same balancing act of extracting simplif
From playlist AATRN 2020
Thomas Weighill - Coarse homotopy groups of warped cones
38th Annual Geometric Topology Workshop (Online), June 15-17, 2021 Thomas Weighill, University of North Carolina at Greensboro Title: Coarse homotopy groups of warped cones Abstract: Various versions of coarse homotopy theory have been around since the beginning of coarse geometry, and s
From playlist 38th Annual Geometric Topology Workshop (Online), June 15-17, 2021

Oliver Röndigs: The slices of Hermitian K-theory (Lecture 1)
The lecture was held within the framework of the (Junior) Hausdorff Trimester Program Topology: Workshop "Hermitian K-theory and trace methods" Abstract: Voevodsky constructed a filtration on the motivic stable homotopy category by measuring how many (de)suspensions with respect to the Ta
From playlist HIM Lectures: Junior Trimester Program "Topology"
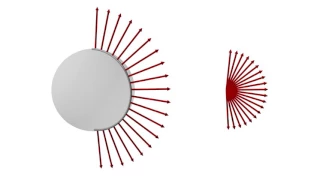
Homotopy elements in the homotopy group π₂(S²) ≅ ℤ. Roman Gassmann and Tabea Méndez suggested some improvements to my original ideas.
From playlist Algebraic Topology
