
Ideals in Ring Theory (Abstract Algebra)
An ideal of a ring is the similar to a normal subgroup of a group. Using an ideal, you can partition a ring into cosets, and these cosets form a new ring - a "factor ring." (Also called a "quotient ring.") After reviewing normal subgroups, we will show you *why* the definition of an ide
From playlist Abstract Algebra
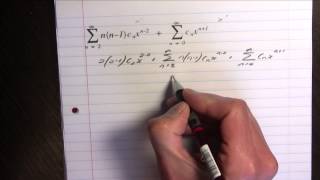
C71 Adding to power series in sigma notation
Simplifying the addition of two power series.
From playlist Differential Equations

RNT1.4. Ideals and Quotient Rings
Ring Theory: We define ideals in rings as an analogue of normal subgroups in group theory. We give a correspondence between (two-sided) ideals and kernels of homomorphisms using quotient rings. We also state the First Isomorphism Theorem for Rings and give examples.
From playlist Abstract Algebra

Benefits Of Six Sigma | Six Sigma Green Belt Training | Simplilearn
The main advantage of Six Sigma compared to other approaches to quality control is that Six Sigma is customer driven. Six Sigma is defined as a limit of 3.4 defects per one million products or service processes, where anything not acceptable to the end customer is considered a defect. 🔥Fr
From playlist Six Sigma Training Videos [2022 Updated]
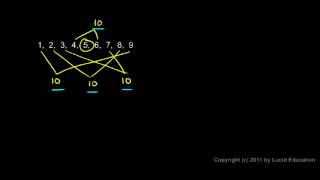
Prealgebra 2.07h - Sigma Notation
A brief introduction to summation notation using the Greek letter Sigma. From the Prealgebra course by Derek Owens. This course is available online at http://www.LucidEducation.com.
From playlist Prealgebra Chapter 2 (Complete chapter)

Benefits of Six Sigma|Summary of Six Sigma Program|Six Sigma Online Certification | Six Sigma Expert
Certified Six Sigma Green Belt, a popular business management strategy is widely used across industries towards quality and process improvement. Simplilearn offers both online Certified Six Sigma Green Belt training and Certified Six Sigma Green Belt classroom training. Accredited by Peopl
From playlist Six Sigma Training Videos [2022 Updated]

Sigma notation for summing series
Support me on Patreon: https://www.patreon.com/mathsaurus How to use sigma notation to describe the process of summing series (adding together the terms in a sequence). Visit http://www.mathsaurus.com/ for more free GCSE and A-level maths videos and resources Visit the Mathsaurus Ama
From playlist C1 C2 Sequences APs and GPs

Landau-Ginzburg - Seminar 2 - Introduction
This seminar series is about the bicategory of Landau-Ginzburg models LG, hypersurface singularities and matrix factorisations. In this second seminar Dan Murfet explains how to compose permutations from a geometric perspective. The webpage for this seminar is https://metauni.org/lg/. Yo
From playlist Landau-Ginzburg seminar

Elliptic Curves - Lecture 19b - Elliptic curves over local fields (the action of inertia)
This video is part of a graduate course on elliptic curves that I taught at UConn in Spring 2021. The course is an introduction to the theory of elliptic curves. More information about the course can be found at the course website: https://alozano.clas.uconn.edu/math5020-elliptic-curves/
From playlist An Introduction to the Arithmetic of Elliptic Curves

on the Brumer-Stark Conjecture (Lecture 3) by Mahesh Kakde
PROGRAM ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (HYBRID) ORGANIZERS: Ashay Burungale (CalTech/UT Austin, USA), Haruzo Hida (UCLA), Somnath Jha (IIT Kanpur) and Ye Tian (MCM, CAS) DATE: 08 August 2022 to 19 August 2022 VENUE: Ramanujan Lecture Hall and online The program pla
From playlist ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (2022)

Kevin Buzzard (lecture 10/20) Automorphic Forms And The Langlands Program [2017]
Full course playlist: https://www.youtube.com/playlist?list=PLhsb6tmzSpiysoRR0bZozub-MM0k3mdFR http://wwwf.imperial.ac.uk/~buzzard/MSRI/ Summer Graduate School Automorphic Forms and the Langlands Program July 24, 2017 - August 04, 2017 Kevin Buzzard (Imperial College, London) https://w
From playlist MSRI Summer School: Automorphic Forms And The Langlands Program, by Kevin Buzzard [2017]

Karim Alexander Adiprasito - 5/6 - Lefschetz, Hodge and combinatorics...
Lefschetz, Hodge and combinatorics: an account of a fruitful cross-pollination Almost 40 years ago, Stanley noticed that some of the deep theorems of algebraic geometry have powerful combinatorial applications. Among other things, he used the hard Lefschetz theorem to rederive Dynkin's t

Nonlinear algebra, Lecture 10: "Invariant Theory", by Bernd Sturmfels
This is the tenth lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences.
From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

Lean Six SIgma Certification for Starters-Giving Edge to your Resume and Career | Webinar -1
Watch Sample Class Recording: http://www.edureka.co/six-sigma-green-belt?utm_source=youtube&utm_medium=webinar&utm_campaign=six-sigma-4-6-2015 Six Sigma is a disciplined, data-driven approach and methodology for eliminating defects (driving toward six standard deviations between the mean
From playlist Webinars by Edureka!

Solving difference equations in sequences It is known that a finite system of algebraic difference equations has a solution in the ring of sequences if and only if the difference ideal it generates contains 1. Moreover, there exists an algorithm that determines whether or not 1 lies in th
From playlist DART X

Karim Alexander Adiprasito - 6/6 - Lefschetz, Hodge and combinatorics...
Lefschetz, Hodge and combinatorics: an account of a fruitful cross-pollination Almost 40 years ago, Stanley noticed that some of the deep theorems of algebraic geometry have powerful combinatorial applications. Among other things, he used the hard Lefschetz theorem to rederive Dynkin's t

Discrete groups in complex hyperbolic geometry (Lecture - 2) by Pierre Will
Geometry, Groups and Dynamics (GGD) - 2017 DATE: 06 November 2017 to 24 November 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The program focuses on geometry, dynamical systems and group actions. Topics are chosen to cover the modern aspects of these areas in which research has b
From playlist Geometry, Groups and Dynamics (GGD) - 2017

Introduction to Series (1 of 2: Interpreting Sigma Notation)
More resources available at www.misterwootube.com
From playlist Modelling Financial Situations

Karim Alexander Adiprasito - 4/6 - Lefschetz, Hodge and combinatorics...
Lefschetz, Hodge and combinatorics: an account of a fruitful cross-pollination Almost 40 years ago, Stanley noticed that some of the deep theorems of algebraic geometry have powerful combinatorial applications. Among other things, he used the hard Lefschetz theorem to rederive Dynkin's t
