
Reciprocal Identities in Trigonometry (Precalculus - Trigonometry 9)
How the reciprocal identities in trigonometry work and how to use them. The major focus will be on connecting the ideas of a Unit circle with Right Triangle Trigonometry. Support: https://www.patreon.com/ProfessorLeonard
From playlist Precalculus - College Algebra/Trigonometry

Even and Odd Trigonometric Identities
This video states and illustrated the even and odd trigonometric identities. It also reviews even and odd functions. Complete Video List at www.mathispower4u.yolasite.com or search them on my blog at www.mathispower4u.wordpress.com
From playlist Reciprocal, Quotient, Negative, and Pythagorean Trigonometric Identities

Evaluating your trig functions and reciprocal functions with a calculator
👉 Learn how to evaluate trigonometric functions using a calculator. To evaluate the trigonometric functions using a calculator, we just punch the necessary buttons on the calculator to obtain the result. While this may seem simple, most calculators only have sine, cosine and tangent avai
From playlist Trigonometric Functions and The Unit Circle

What are the reciprocal identities of trigonometric functions
👉 Learn all about the different trigonometric identities and how they can be used to evaluate, verify, simplify and solve trigonometric equations. The identities discussed in this playlist will involve the quotient, reciprocal, half-angle, double angle, Pythagorean, sum, and difference. I
From playlist Learn About Trigonometric Identities

What are co function identities
👉 Learn all about the different trigonometric identities and how they can be used to evaluate, verify, simplify and solve trigonometric equations. The identities discussed in this playlist will involve the quotient, reciprocal, half-angle, double angle, Pythagorean, sum, and difference. I
From playlist Learn About Trigonometric Identities

Trigonometry II: Cosecant, Secant, and Cotangent
Are you interested in math or physics tutoring for you or someone you know? Please check out my website for more details of my registered business, or give me a call or email anytime! https://www.whatthehectogon.com/ +1 (973) 597-8775 sam@whatthehectogon.com In this video, I define the
From playlist Trigonometry

Aaron Sidford: Introduction to interior point methods for discrete optimization, lecture II
Over the past decade interior point methods (IPMs) have played a pivotal role in mul- tiple algorithmic advances. IPMs have been leveraged to obtain improved running times for solving a growing list of both continuous and combinatorial optimization problems including maximum flow, bipartit
From playlist Summer School on modern directions in discrete optimization
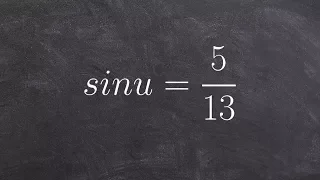
Evaluating the difference of two angles for the cosine function
👉 Learn how to evaluate the secant of the sum or difference of two angles using the sum/difference formulas. To do this, we first use the Pythagoras theorem to obtain all the sides of the right triangle in the unit circle. Recall that secant is the reciprocal of cosine, so when we know th
From playlist Sum and Difference Formulas

Aaron Sidford: Introduction to interior point methods for discrete optimization, lecture III
Over the past decade interior point methods (IPMs) have played a pivotal role in mul- tiple algorithmic advances. IPMs have been leveraged to obtain improved running times for solving a growing list of both continuous and combinatorial optimization problems including maximum flow, bipartit
From playlist Summer School on modern directions in discrete optimization

Lecture 16 | Convex Optimization I (Stanford)
Professor Stephen Boyd, of the Stanford University Electrical Engineering department, lectures on how equality constrained minimization is utilized in electrical engineering for the course, Convex Optimization I (EE 364A). Convex Optimization I concentrates on recognizing and solving co
From playlist Lecture Collection | Convex Optimization
Towards a theory of non-commutative optimization...… -Rafael Oliveira
Computer Science/Discrete Mathematics Seminar I Topic: Towards a theory of non-commutative optimization: geodesic 1st and 2nd order methods for moment maps and polytopes Speaker: Rafael Oliveira Affiliation:University of Toronto Date: October 22, 2019 For more video please visit http://v
From playlist Mathematics

Operator Scaling via Geodesically Convex Optimization, Invariant Theory... - Yuanzhi Li
Optimization, Complexity and Invariant Theory Topic: Operator Scaling via Geodesically Convex Optimization, Invariant Theory and Polynomial Identity Testing Speaker: Yuanzhi Li Affiliation: Princeton University Date: June 7. 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics
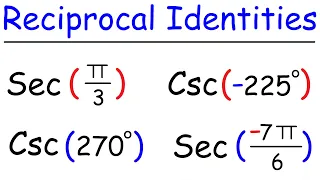
Reciprocal Identities - Evaluating Secant and Cosecant Functions
This trigonometry video tutorial explains how to use the reciprocal identities to evaluate trigonometric functions such as secant and cosecant. This video contains plenty of practice example problems.
From playlist New Precalculus Video Playlist

Xavier Bresson: "The Transformer Network for the Traveling Salesman Problem"
Deep Learning and Combinatorial Optimization 2021 "The Transformer Network for the Traveling Salesman Problem" Xavier Bresson - Nanyang Technological University, Singapore Abstract: The Traveling Salesman Problem (TSP) is the most popular and most studied combinatorial problem, starting
From playlist Deep Learning and Combinatorial Optimization 2021

Polynomial Identity Testing via Optimization: algorithms by Rafael Oliveira
Discussion Meeting Workshop on Algebraic Complexity Theory  ORGANIZERS Prahladh Harsha, Ramprasad Saptharishi and Srikanth Srinivasan DATE & TIME 25 March 2019 to 29 March 2019 VENUE Madhava Lecture Hall, ICTS Bangalore Algebraic complexity aims at understanding the computationa
From playlist Workshop on Algebraic Complexity Theory 2019

Evaluating Expressions Involving Inverse Cosecant, Inverse Secant, and Inverse Cotangent
Evaluate inverse trigonometric expression. http://mathispower4u.wordpress.com/
From playlist Inverse Trigonometric Functions

Nexus Trimester - Alexandre d'Aspremont (École Normale Supérieure)
An Optimal Affine Invariant Smooth Minimization Algorithm Alexandre d'Aspremont (École Normale Supérieure) March 18, 2016 Abstract: We formulate an affine invariant implementation of the algorithm in (Nesterov, 1983). We show that the complexity bound is then proportional to an affine in
From playlist 2016-T1 - Nexus of Information and Computation Theory - CEB Trimester
Lek-Heng Lim: "What is a tensor? (Part 2/2)"
Watch part 1/2 here: https://youtu.be/MkYEh0UJKcE Tensor Methods and Emerging Applications to the Physical and Data Sciences Tutorials 2021 "What is a tensor? (Part 2/2)" Lek-Heng Lim - University of Chicago, Statistics Abstract: We discuss the three best-known definitions of a tensor:
From playlist Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021

Evaluating the sum and difference for Secant
👉 Learn how to evaluate the secant of the sum or difference of two angles using the sum/difference formulas. To do this, we first use the Pythagoras theorem to obtain all the sides of the right triangle in the unit circle. Recall that secant is the reciprocal of cosine, so when we know th
From playlist Sum and Difference Formulas

Jianfeng Lin - On monopole Lefschetz number
June 29, 2018 - This talk was part of the 2018 RTG mini-conference Low-dimensional topology and its interactions with symplectic geometry
From playlist 2018 RTG mini-conference on low-dimensional topology and its interactions with symplectic geometry II