
Polynomials and Polynomial Terminology (L3.1)
This video covers the basic vocabulary involving polynomials. Video content created Jenifer Bohart, William Meacham, Judy Sutor, and Donna Guhse from SCC (CC-BY 4.0)
From playlist Introduction to Polynomials

Classify a polynomial then determining if it is a polynomial or not
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?

Determining if a equation is a polynomial or not
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?

Is it a polynomial with two variables
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?

Separation of variables and the Schrodinger equation
A brief explanation of separation of variables, application to the time-dependent Schrodinger equation, and the solution to the time part. (This lecture is part of a series for a course based on Griffiths' Introduction to Quantum Mechanics. The Full playlist is at http://www.youtube.com/
From playlist Mathematical Physics II - Youtube

Representation of finite groups over arbitrary fields by Ravindra S. Kulkarni
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

How to reorder and classify a polynomial based on it's degree and number of terms
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different integer exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials | Equations

Learn how to identify if a function is a polynomial and identify the degree and LC
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (4 of 92) The Schrodinger Eqn. "Derived"
Visit http://ilectureonline.com for more math and science lectures! In this video I will “derive” the Schrodinger equation using y(x,y)=Acos(kx-wt). Next video in this series can be seen at: https://youtu.be/GyKk2-0JZ48
From playlist PHYSICS 66.1 QUANTUM MECHANICS - SCHRODINGER EQUATION

Alexander Moll: A new spectral theory for Schur polynomials and applications
Abstract: After Fourier series, the quantum Hopf-Burgers equation vt+vvx=0 with periodic boundary conditions is equivalent to a system of coupled quantum harmonic oscillators, which may be prepared in Glauber's coherent states as initial conditions. Sending the displacement of each oscilla
From playlist Combinatorics
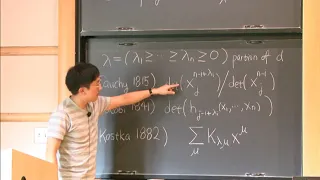
Logarithmic concavity of Schur polynomials - June Huh
Members' Seminar Topic: Logarithmic concavity of Schur polynomials Speaker: June Huh Visiting Professor, School of Mathematics Date: October 7, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

Mod-01 Lec-36 Spectral Theorem
Elementary Numerical Analysis by Prof. Rekha P. Kulkarni,Department of Mathematics,IIT Bombay.For more details on NPTEL visit http://nptel.ac.in
From playlist NPTEL: Elementary Numerical Analysis | CosmoLearning Mathematics

Learn how to classify and identify the lc and degree of a polynomial
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different interger exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials

Vera Serganova: Capelli eigenvalue problem for Lie superalgebras and supersymetric polynominals
Abstract: We study invariant differential operators on representations of supergroups associated with simple Jordan superalgebras, in the classical case this problem goes back to Kostant. Eigenvalues of Capelli differential operators give interesting families of polynomials such as super J
From playlist Mathematical Physics

Vitaly Bergelson: Mutually enriching connections between ergodic theory and combinatorics - part 6
Abstract : * The early results of Ramsey theory : Hilbert's irreducibility theorem, Dickson-Schur work on Fermat's equation over finite fields, van der Waerden's theorem, Ramsey's theoremand its rediscovery by Erdos and Szekeres. * Three main principles of Ramsey theory : First principl
From playlist Jean-Morlet Chair - Lemanczyk/Ferenczi

Vitaly Bergelson: Mutually enriching connections between ergodic theory and combinatorics - part 1
Abstract : * The early results of Ramsey theory : Hilbert's irreducibility theorem, Dickson-Schur work on Fermat's equation over finite fields, van der Waerden's theorem, Ramsey's theoremand its rediscovery by Erdos and Szekeres. * Three main principles of Ramsey theory : First principl
From playlist Jean-Morlet Chair - Lemanczyk/Ferenczi

Vitaly Bergelson: Mutually enriching connections between ergodic theory and combinatorics - part 7
Abstract : * The early results of Ramsey theory : Hilbert's irreducibility theorem, Dickson-Schur work on Fermat's equation over finite fields, van der Waerden's theorem, Ramsey's theoremand its rediscovery by Erdos and Szekeres. * Three main principles of Ramsey theory : First principl
From playlist Jean-Morlet Chair - Lemanczyk/Ferenczi

Vitaly Bergelson: Mutually enriching connections between ergodic theory and combinatorics - part 2
Abstract : * The early results of Ramsey theory : Hilbert's irreducibility theorem, Dickson-Schur work on Fermat's equation over finite fields, van der Waerden's theorem, Ramsey's theoremand its rediscovery by Erdos and Szekeres. * Three main principles of Ramsey theory : First principl
From playlist Jean-Morlet Chair - Lemanczyk/Ferenczi

Dealing with Schrodinger's Equation - The Hamiltonian
https://www.patreon.com/edmundsj If you want to see more of these videos, or would like to say thanks for this one, the best way you can do that is by becoming a patron - see the link above :). And a huge thank you to all my existing patrons - you make these videos possible. Schrodinger's
From playlist Quantum Mechanics

Vitaly Bergelson: Mutually enriching connections between ergodic theory and combinatorics- part 4
Abstract : * The early results of Ramsey theory : Hilbert's irreducibility theorem, Dickson-Schur work on Fermat's equation over finite fields, van der Waerden's theorem, Ramsey's theoremand its rediscovery by Erdos and Szekeres. * Three main principles of Ramsey theory : First principl
From playlist Jean-Morlet Chair - Lemanczyk/Ferenczi