
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (17 of 92) How to Use Schrod. Eqn: 2
Visit http://ilectureonline.com for more math and science lectures! In this video I will show how to use the Schrodinger's equation, part 2/2. Next video in this series can be seen at: https://youtu.be/kO9JZgVXqyU
From playlist PHYSICS 66.1 QUANTUM MECHANICS - SCHRODINGER EQUATION

Acoustic Standing Waves and the Levitation of Small Objects
Acoustic levitation meets schlieren imaging: By reflecting a sound wave back onto itself, one can secure a standing wave if the distance between the source of the sound and the reflector is equal to an integral number of half wavelengths. In this demonstration we use 28 kHz ultrasound whos
From playlist Oscillations and Waves

Yuli Rudyak (2/8/2018): Maps of Degree 1 and Lusternik-Schnirelmann Category
Given a map f:M→N of degree 1 of closed manifolds, is it true that the Lusternik-Schnirelmann category of the range of the map is not more that the category of the domain? We discuss this and some related questions.
From playlist Wright College Topological Robotics Symposium 2018

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (13 of 92) Time & Position Dependencies 2/3
Visit http://ilectureonline.com for more math and science lectures! In this video I will find C=?, of the position part of the Schrodinger's equation by using the time dependent part of Schrodinger's equation, part 2/3. Next video in this series can be seen at: https://youtu.be/1mxipWt-W
From playlist PHYSICS 66.1 QUANTUM MECHANICS - SCHRODINGER EQUATION

Nursultan Kuanyshov: Lusternik-Schnirelmann category of group homomorphism
Nursultan Kuanyshov, University of Florida Title: Lusternik-Schnirelmann category of group homomorphism We prove the equality $\text{cat}(\phi)=\text{cd}(\phi)$ for homomorphisms $\phi:\Gamma\rightarrow \Lambda$ of a torsion free finitely generated nilpotent groups $\Gamma$ to an arbitrary
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

Enrique Macias-Virgo (5/27/21): Homotopic distance and Generalized motion planning
Lusternik-Schnirelmann category and topological complexity are particular cases of a more general notion, that we call homotopic distance between two maps. As a consequence, several properties of those invariants can be proved in a unified way and new results arise. For instance, we prove
From playlist Topological Complexity Seminar

Rustam Sadykov (1/28/21): On the Lusternik-Schnirelmann theory of 4-manifolds
Title: On the Lusternik-Schnirelmann theory of 4-manifolds Abstract: I will discuss various versions of the Lusternik-Schnirelman category involving covers and fillings of 4-manifolds by various sets. In particular, I will discuss Gay-Kirby trisections, which are certain decompositions o
From playlist Topological Complexity Seminar

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (3 of 92) The Wave Equation
Visit http://ilectureonline.com for more math and science lectures! In this video I will show that Schrodinger equation as a wave equation satisfying the general wave equation. Next video in this series can be seen at: https://youtu.be/mFGkuhxu5Bw
From playlist PHYSICS 66.1 QUANTUM MECHANICS - SCHRODINGER EQUATION

My Favorite Theorem: The Borsuk-Ulam Theorem
Many thanks for 10k subscribers! Fun video for you from Topology: The Borsuk-Ulam Theorem. One interpretation of this is that on the surface of the earth, there must be some point where it and its antipode (the spot exactly opposite it) have the exact same temperature and pressure. More ge
From playlist Cool Math Series

Alexander Dranishnikov (9/22/22): On the LS-category of group homomorphisms
In 50s Eilenberg and Ganea proved that the Lusternik-Schnirelmann category of a discrete group Γ equals its cohomological dimension, cat(Γ) = cd(Γ). We discuss a possibility of the similar equality cat(φ) = cd(φ) for group homomorphisms φ : Γ → Λ. We prove this equality for some classes of
From playlist Topological Complexity Seminar

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (5 of 92) The Schrodinger Eqn. in 1-D (1/3)
Visit http://ilectureonline.com for more math and science lectures! In this video I will derive the Schrodinger equations for a particle in 1-dimension (Part 1 of 3). Next video in this series can be seen at: https://youtu.be/2PdLQeUkd7I
From playlist PHYSICS 66.1 QUANTUM MECHANICS - SCHRODINGER EQUATION

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (7 of 92) The Schrodinger Eqn. in 1-D (3/3)
Visit http://ilectureonline.com for more math and science lectures! In this video I will derive the Schrodinger equations for a particle in 1-dimension (Part 3 of 3). Next video in this series can be seen at: https://youtu.be/SyBdlw5wNLU
From playlist PHYSICS 66.1 QUANTUM MECHANICS - SCHRODINGER EQUATION

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (14 of 92) Time & Position Dependencies 3/3
Visit http://ilectureonline.com for more math and science lectures! In this video I will find the time independent Schrodinger's equation for a particle in 1-dimension, part 3/3. Next video in this series can be seen at: https://youtu.be/6HcPTgc84O8
From playlist PHYSICS 66.1 QUANTUM MECHANICS - SCHRODINGER EQUATION

Clara Löh (5/28/22): Lower multiplicity bounds via classifying spaces
We consider variations of the Lusternik--Schnirelmann category, based on open covers satisfying constraints on the level of the fundamental group. Such LS-category invariants can be analysed through equivariant methods. For example, classifying spaces for families of subgroups can be used
From playlist Topological Complexity Seminar

Physics - Ch 66.5 Quantum Mechanics: The Hydrogen Atom (20 of 78) Schrodinger in Spherical 4
Visit http://ilectureonline.com for more math and science lectures! In this video I will manipulate the 3 equation we found from the 2 previous videos into a more manageable format.write the Schrodinger Equation as a product of 3 separate equations. In the previous video we found the func
From playlist PHYSICS 66.5 QUANTUM MECHANICS: THE HYDROGEN ATOM

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (12 of 92) Time & Position Dependencies 1/3
Visit http://ilectureonline.com for more math and science lectures! In this video I will separate the time and position dependencies of the Schrodinger's equation, part 1/3. Next video in this series can be seen at: https://youtu.be/djlpmDUtIZY
From playlist PHYSICS 66.1 QUANTUM MECHANICS - SCHRODINGER EQUATION

Lec 7 | MIT 3.320 Atomistic Computer Modeling of Materials
Technical Aspects of Density Functional Theory View the complete course at: http://ocw.mit.edu/3-320S05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 3.320 Atomistic Computer Modeling of Materials

Robert Seiringer: The local density approximation in density functional theory
We present a mathematically rigorous justification of the Local Density Approximation in density functional theory. We provide a quantitative estimate on the difference between the grand-canonical Levy-Lieb energy of a given density (the lowest possible energy of all quantum st
From playlist Mathematical Physics
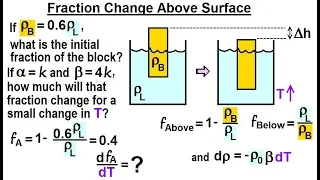
Physics - Ch 22A Test Your Knowledge: Thermal Expansion (4 of 20) Fractional Change Above Surface
Visit http://ilectureonline.com for more math and science lectures! We will find what is the initial fraction of the block above the liquid. And how much will that fraction change for a small change in temperature. To donate: http://www.ilectureonline.com/donate https://www.patreon.com/u
From playlist PHYSICS 22A TEST YOUR KNOWLEDGE: THERMAL EXPANSION

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (82 of 92) Barrier: Boundary Conditions
Visit http://ilectureonline.com for more math and science lectures! In this video I will look at the boundary conditions on either side of the barrier when x=0 and x=L, such the equation of the motion of the particle on the left-side and the right-side of the boundary should match at x=0
From playlist PHYSICS 66.1 QUANTUM MECHANICS - SCHRODINGER EQUATION