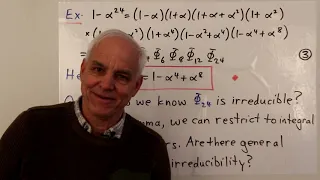
Irreducibility and the Schoenemann-Eisenstein criterion | Famous Math Probs 20b | N J Wildberger
In the context of defining and computing the cyclotomic polynumbers (or polynomials), we consider irreducibility. Gauss's lemma connects irreducibility over the integers to irreducibility over the rational numbers. Then we describe T. Schoenemann's irreducibility criterion, which uses some
From playlist Famous Math Problems

Dealing with Schrodinger's Equation - The Hamiltonian
https://www.patreon.com/edmundsj If you want to see more of these videos, or would like to say thanks for this one, the best way you can do that is by becoming a patron - see the link above :). And a huge thank you to all my existing patrons - you make these videos possible. Schrodinger's
From playlist Quantum Mechanics

The Schrodinger Equation is (Almost) Impossible to Solve.
Sure, the equation is easily solvable for perfect / idealized systems, but almost impossible for any real systems. The Schrodinger equation is the governing equation of quantum mechanics, and determines the relationship between a system, its surroundings, and a system's wave function. Th
From playlist Quantum Physics by Parth G

Srinivasa Varadhan: A Short History of Large Deviations
This lecture was held by Abel Laureate Srinivasa S.R. Varadhan at The University of Oslo, May 24, 2007 and was part of the Abel Prize Lectures in connection with the Abel Prize Week celebrations. Program for the Abel Lectures 2007 1. “A Short History of Large Deviations” by Srinivasa V
From playlist Abel Lectures

Separation of variables and the Schrodinger equation
A brief explanation of separation of variables, application to the time-dependent Schrodinger equation, and the solution to the time part. (This lecture is part of a series for a course based on Griffiths' Introduction to Quantum Mechanics. The Full playlist is at http://www.youtube.com/
From playlist Mathematical Physics II - Youtube

Inflation (Lecture 3) by Paolo Creminelli
Program Cosmology - The Next Decade ORGANIZERS : Rishi Khatri, Subha Majumdar and Aseem Paranjape DATE : 03 January 2019 to 25 January 2019 VENUE : Ramanujan Lecture Hall, ICTS Bangalore The great observational progress in cosmology has revealed some very intriguing puzzles, the most i
From playlist Cosmology - The Next Decade

A quantum particle in a periodic egg carton potential
This simulation of a quantum particle in a periodic particle explores a new visualization, in which the z-coordinate is the sum of the potential, and another quantity related to the wave function (either its real part, or its modulus squared). There is a detailed theory on Schrödinger's eq
From playlist Schrödinger's equation

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (13 of 92) Time & Position Dependencies 2/3
Visit http://ilectureonline.com for more math and science lectures! In this video I will find C=?, of the position part of the Schrodinger's equation by using the time dependent part of Schrodinger's equation, part 2/3. Next video in this series can be seen at: https://youtu.be/1mxipWt-W
From playlist PHYSICS 66.1 QUANTUM MECHANICS - SCHRODINGER EQUATION

The Schrodinger equation made simple | Linearity
We've talked about the quantum state plenty- but what happens to it over time? That's exactly the question the Schrodinger equation solves. This video we talk about 'Linearity'. In the next video we discuss the equation itself and its derivation. Click here fore that: https://youtu.be/DEgW
From playlist Quantum Mechanics (all the videos)

A quantum particle starting in a well of a periodic egg carton potential
Like the video https://youtu.be/DzIZwCeaVkM this one shows a simulation of a quantum particle in a periodic potential. The point of view rotates around the potential landscape, which remains fixed in space. While on the previous video, the initial state was a Gaussian wave packet located n
From playlist Schrödinger's equation

Schrodinger's Equation for wave functions in Quantum Physics. My Patreon Page is at https://www.patreon.com/EugeneK
From playlist Physics

Calculus 1 (Stewart) Ep 22, Mean Value Theorem (Oct 28, 2021)
This is a recording of a live class for Math 1171, Calculus 1, an undergraduate course for math majors (and others) at Fairfield University, Fall 2021. The textbook is Stewart. PDF of the written notes, and a list of all episodes is at the class website. Class website: http://cstaecker.f
From playlist Math 1171 (Calculus 1) Fall 2021

Equidistribution of Unipotent Random Walks on Homogeneous spaces by Emmanuel Breuillard
PROGRAM : ERGODIC THEORY AND DYNAMICAL SYSTEMS (HYBRID) ORGANIZERS : C. S. Aravinda (TIFR-CAM, Bengaluru), Anish Ghosh (TIFR, Mumbai) and Riddhi Shah (JNU, New Delhi) DATE : 05 December 2022 to 16 December 2022 VENUE : Ramanujan Lecture Hall and Online The programme will have an emphasis
From playlist Ergodic Theory and Dynamical Systems 2022

What is Green's theorem? Chris Tisdell UNSW
This lecture discusses Green's theorem in the plane. Green's theorem not only gives a relationship between double integrals and line integrals, but it also gives a relationship between "curl" and "circulation". In addition, Gauss' divergence theorem in the plane is also discussed, whic
From playlist Vector Calculus @ UNSW Sydney. Dr Chris Tisdell

Real Analysis Ep 32: The Mean Value Theorem
Episode 32 of my videos for my undergraduate Real Analysis course at Fairfield University. This is a recording of a live class. This episode is more about the mean value theorem and related ideas. Class webpage: http://cstaecker.fairfield.edu/~cstaecker/courses/2020f3371/ Chris Staecker
From playlist Math 3371 (Real analysis) Fall 2020

Pythagorean theorem - What is it?
► My Geometry course: https://www.kristakingmath.com/geometry-course Pythagorean theorem is super important in math. You will probably learn about it for the first time in Algebra, but you will literally use it in Algebra, Geometry, Trigonometry, Precalculus, Calculus, and beyond! That’s
From playlist Geometry

Wolfram Physics Project: Working Session Sept. 15, 2020 [Physicalization of Metamathematics]
This is a Wolfram Physics Project working session on metamathematics and its physicalization in the Wolfram Model. Begins at 10:15 Originally livestreamed at: https://twitch.tv/stephen_wolfram Stay up-to-date on this project by visiting our website: http://wolfr.am/physics Check out the
From playlist Wolfram Physics Project Livestream Archive

Johnathan Bush (7/8/2020): Borsuk–Ulam theorems for maps into higher-dimensional codomains
Title: Borsuk–Ulam theorems for maps into higher-dimensional codomains Abstract: I will describe Borsuk-Ulam theorems for maps of spheres into higher-dimensional codomains. Given a continuous map from a sphere to Euclidean space, we say the map is odd if it respects the standard antipodal
From playlist AATRN 2020

Worldwide Calculus: Extrema and the Mean Value Theorem
Lecture on 'Extrema and the Mean Value Theorem' from 'Worldwide Differential Calculus' and 'Worldwide AP Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
From playlist Worldwide Single-Variable Calculus for AP®

What is the Schrödinger Equation? A basic introduction to Quantum Mechanics
This video provides a basic introduction to the Schrödinger equation by exploring how it can be used to perform simple quantum mechanical calculations. After explaining the basic structure of the equation, the infinite square well potential is used as a case study. The separation of variab
From playlist Quantum Physics