This lecture is on Introduction to Higher Mathematics (Proofs). For more see http://calculus123.com.
From playlist Proofs

Math 139 Fourier Analysis Lecture 09: L^2 convergence of the Fourier Series
L^2 convergence of Fourier Series: little l^2; l^2 is a vector space; the space of integrable functions on the circle; Fourier series of an integrable function converges to the function in the sense of L^2
From playlist Course 8: Fourier Analysis

This video explains the definition of a vector space and provides examples of vector spaces.
From playlist Vector Spaces

Introduction to Metric Spaces - Definition of a Metric. - The metric on R - The Euclidean Metric on R^n - A metric on the set of all bounded functions - The discrete metric
From playlist Topology

This video is about metric spaces and some of their basic properties.
From playlist Basics: Topology
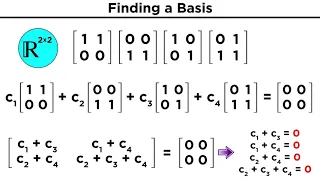
Now we know about vector spaces, so it's time to learn how to form something called a basis for that vector space. This is a set of linearly independent vectors that can be used as building blocks to make any other vector in the space. Let's take a closer look at this, as well as the dimen
From playlist Mathematics (All Of It)

What exactly is space? Brian Greene explains what the "stuff" around us is. Subscribe to our YouTube Channel for all the latest from World Science U. Visit our Website: http://www.worldscienceu.com/ Like us on Facebook: https://www.facebook.com/worldscienceu Follow us on Twitter: https:
From playlist Science Unplugged: Physics

After our introduction to matrices and vectors and our first deeper dive into matrices, it is time for us to start the deeper dive into vectors. Vector spaces can be vectors, matrices, and even function. In this video I talk about vector spaces, subspaces, and the porperties of vector sp
From playlist Introducing linear algebra

From playlist Unlisted LA Videos

Localization of Spaces by Somnath Basu
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)

Noncommutative Geometric Invariant Theory (Lecture 2) by Arvid Siqveland
PROGRAM :SCHOOL ON CLUSTER ALGEBRAS ORGANIZERS :Ashish Gupta and Ashish K Srivastava DATE :08 December 2018 to 22 December 2018 VENUE :Madhava Lecture Hall, ICTS Bangalore In 2000, S. Fomin and A. Zelevinsky introduced Cluster Algebras as abstractions of a combinatoro-algebra
From playlist School on Cluster Algebras 2018

Schemes 41: Morphisms to projective space
This lecture is part of an online course on algebraic geometry based on chapter II of "algebraic geometry" by Hartshorne. We discuss morphisms of a scheme to projective space, showing that they correspond to a line bundle with a set of sections generating it.
From playlist Algebraic geometry II: Schemes

Extremal Combinatorics with Po-Shen Loh - 04/22 Wed
Carnegie Mellon University is protecting the community from the COVID-19 pandemic by running courses online for the Spring 2020 semester. This is the video stream for Po-Shen Loh’s PhD-level course 21-738 Extremal Combinatorics. Professor Loh will not be able to respond to questions or com
From playlist CMU PhD-Level Course 21-738 Extremal Combinatorics

Sylvie Monniaux: Uniqueness of the Boussinesq system in critical spaces using maximal regularity
We prove uniqueness of the solutions ($u$, velocity and $\theta$, temperature) of the Boussinesq system in the whole space ${\mathbb{R}}^3$ in the critical functional spaces: continuous in time with values in $L^3$ for the velocity and $L^2$ in time with values in $L^{3/2}$ in space for th
From playlist Women at CIRM

Simon Foucart: Essentials of Compressive Sensing (Lecture 2)
Compressive Sensing has recently had a tremendous impact in science and engineering, because it revealed the theoretical possibility of acquiring structured high-dimensional objects using much less information than previously expected, and more importantly because it provided practical pro
From playlist HIM Lectures: Trimester Program "Mathematics of Signal Processing"

A simple proof of a reverse Minkowski inequality - Noah Stephens-Davidowitz
Computer Science/Discrete Mathematics Seminar II Topic: A simple proof of a reverse Minkowski inequality Speaker: Noah Stephens-Davidowitz Affiliation: Visitor, School of Mathematics Date: April 17, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

More On Lp And L2 Spaces Part 1
Lecture with Ole Christensen. Kapitler: 00:00 - Introduction; 05:00 - Complication With Norm On Lp Spaces; 11:30 - Dis/Advantages With Cc,Co,Lp Spaces; 20:00 - Why Not Only Use L1?; 22:00 - Cc Is Dense In L1; 26:00 - Recall Hilbert Spaces; 28:00 - L2 Is A Hilbert Space ; 39:00 - Operators
From playlist DTU: Mathematics 4 Real Analysis | CosmoLearning.org Math

Jesse Peterson: Von Neumann algebras and lattices in higher-rank groups, Lecture 1
Mini course of the conference YMC*A, August 2021, University of Münster. Lecture 1: Background on von Neumann algebras. Abstract: We’ll briskly review basic properties of semi-finite von Neumann algebras. The standard representation, completely positive maps, group von Neumann algebras, th
From playlist YMC*A 2021

