
Theory of numbers: Congruences: Euler's theorem
This lecture is part of an online undergraduate course on the theory of numbers. We prove Euler's theorem, a generalization of Fermat's theorem to non-prime moduli, by using Lagrange's theorem and group theory. As an application of Fermat's theorem we show there are infinitely many prim
From playlist Theory of numbers

Calculus 5.3 The Fundamental Theorem of Calculus
My notes are available at http://asherbroberts.com/ (so you can write along with me). Calculus: Early Transcendentals 8th Edition by James Stewart
From playlist Calculus

What is Stokes theorem? - Formula and examples
► My Vectors course: https://www.kristakingmath.com/vectors-course Where Green's theorem is a two-dimensional theorem that relates a line integral to the region it surrounds, Stokes theorem is a three-dimensional version relating a line integral to the surface it surrounds. For that reaso
From playlist Vectors
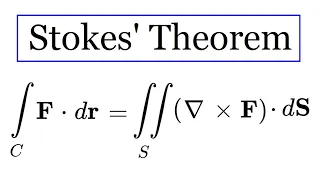
In this video, I present another example of Stokes theorem, this time using it to calculate the line integral of a vector field. It is a very useful theorem that arises a lot in physics, for example in Maxwell's equations. Other Stokes Example: https://youtu.be/-fYbBSiqvUw Yet another Sto
From playlist Vector Calculus

Understanding and computing the Riemann zeta function
In this video I explain Riemann's zeta function and the Riemann hypothesis. I also implement and algorithm to compute the return values - here's the Python script:https://gist.github.com/Nikolaj-K/996dba1ff1045d767b10d4d07b1b032f
From playlist Programming

Theory of numbers: Gauss's lemma
This lecture is part of an online undergraduate course on the theory of numbers. We describe Gauss's lemma which gives a useful criterion for whether a number n is a quadratic residue of a prime p. We work it out explicitly for n = -1, 2 and 3, and as an application prove some cases of Di
From playlist Theory of numbers

Calculus - The Fundamental Theorem, Part 3
The Fundamental Theorem of Calculus. Specific examples of simple functions, and how the antiderivative of these functions relates to the area under the graph.
From playlist Calculus - The Fundamental Theorem of Calculus

Wolfram Physics Project: Working Session Tuesday, Nov. 16, 2021 [Metamathematics]
This is a Wolfram Physics Project working session on metamathematics in the Wolfram Model. Originally livestreamed at: https://twitch.tv/stephen_wolfram Stay up-to-date on this project by visiting our website: http://wolfr.am/physics Check out the announcement post: http://wolfr.am/
From playlist Wolfram Physics Project Livestream Archive

Michael Harris "Shimura varieties and the search for a Langlands transform" [2012]
Michael Harris, Institut de mathématiques de Jussieu "Shimura varieties and the search for a Langlands transform" The Langlands reciprocity conjectures predict the existence of a correspondence between certain classes of representations of Galois groups of number fields and automorphic re
From playlist Number Theory

Primes and Equations | Richard Taylor
Richard Taylor, Professor, School of Mathematics, Institute for Advanced Study http://www.ias.edu/people/faculty-and-emeriti/taylor One of the oldest subjects in mathematics is the study of Diophantine equations, i.e., the study of whole number (or fractional) solutions to polynomial equ
From playlist Mathematics

Bourgain–Delbaen ℒ_∞-spaces and the scalar-plus-compact property – R. Haydon & S. Argyros – ICM2018
Analysis and Operator Algebras Invited Lecture 8.16 Bourgain–Delbaen ℒ_∞-spaces, the scalar-plus-compact property and related problems Richard Haydon & Spiros Argyros Abstract: We outline a general method of constructing ℒ_∞-spaces, based on the ideas of Bourgain and Delbaen, showing how
From playlist Analysis & Operator Algebras
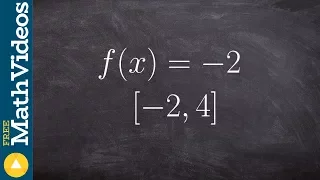
What is the max and min of a horizontal line on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Richard Stanley - Increasing and decreasing subsequences (2006)
slides for this talk: https://www.mathunion.org/fileadmin/IMU/Videos/ICM2006/tars/stanley2006.pdf ICM Madrid Videos 24.08.2006 Increasing and decreasing subsequences Richard P. Stanley Massachusetts Institute of Technology, Cambridge, USA 24-Aug-06 · 09:00-10:00 h https://www.mathunion.
From playlist Mathematics

Generic K3 categories and Hodge theory - Daniel Huybrechts
Daniel Huybrechts University of Bonn September 16, 2014 In this talk I will focus on two examples of K3 categories: bounded derived categories of (twisted) coherent sheaves and K3 categories associated with smooth cubic fourfolds. The group of autoequivalences of the former has been inten
From playlist Mathematics

Davesh Maulik - Stable Pairs and Gopakumar-Vafa Invariants 1/5
In the first part of the course, I will give an overview of Donaldson-Thomas theory for Calabi-Yau threefold geometries, and its cohomological refinement. In the second part, I will explain a conjectural ansatz (from joint work with Y. Toda) for defining Gopakumar-Vafa invariants via modul
From playlist 2021 IHES Summer School - Enumerative Geometry, Physics and Representation Theory

Calculus - The Fundamental Theorem, Part 1
The Fundamental Theorem of Calculus. First video in a short series on the topic. The theorem is stated and two simple examples are worked.
From playlist Calculus - The Fundamental Theorem of Calculus

8ECM Invited Lecture: Richard Nickl
From playlist 8ECM Invited Lectures

Learn Math Proofs with this FREE Book
In this video I go over a book that you can use to teach yourself how to write mathematical proofs. Several people have left very positive comments about this book and I agree with them, it's a great book! This book is available for FREE in pdf version. You can also purchase softcover and
From playlist Book Reviews
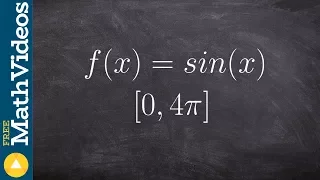
How to determine the max and min of a sine on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Operational K-theory - Sam Payne
Sam Payne March 13, 2015 Workshop on Chow groups, motives and derived categories More videos on http://video.ias.edu
From playlist Mathematics