
This video is about The Coordinate Plane
From playlist Integers and The Coordinate Plane

RT6. Representations on Function Spaces
Representation Theory: We note how to transfer a group action of a group G on a set X to a group action on F(X), the functions on X. Because F(X) is a vector space, we obtain a representation of the group, and we can apply previous techniques. In particular, the group acts on itself in
From playlist Representation Theory

From playlist 2. Attributes of Functions

RT4.1. Constructions from Linear Algebra (Expanded)
Representation Theory: We apply techniques from linear algebra to construct new representations from old ones. Constructions include direct sums, dual spaces, tensor products, and Hom spaces. Course materials, including problem sets and solutions, available at http://mathdoctorbob.org/U
From playlist Representation Theory

Direct Variation and the Coordinate Plane // Math Minute [#19] [ALGEBRA]
The coordinate plane is nothing more than two number lines placed perpendicularly to each other at a particular point (0,0). Since we saw a few videos ago (https://youtu.be/v_aaVdxGRw8) that multiplication can represent scaling from one number line to another, we should be able to use the
From playlist Math Minutes

Coordinate vectors and change of coordinates matrix. Check out my Matrix Algebra playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmAIZGo2l8SWvsHeeCLzamx0 Subscribe to my channel: https://www.youtube.com/channel/UCoOjTxz-u5zU0W38zMkQIFw
From playlist Linear Transformations

Representation theory: Introduction
This lecture is an introduction to representation theory of finite groups. We define linear and permutation representations, and give some examples for the icosahedral group. We then discuss the problem of writing a representation as a sum of smaller ones, which leads to the concept of irr
From playlist Representation theory

Definition of spherical coordinates | Lecture 33 | Vector Calculus for Engineers
We define the relationship between Cartesian coordinates and spherical coordinates; the position vector in spherical coordinates; the volume element in spherical coordinates; the unit vectors; and how to differentiate the spherical coordinate unit vectors. Join me on Coursera: https://www
From playlist Vector Calculus for Engineers

Quiver moduli and applications, Markus Reineke (Bochum), Lecture 3
Quiver moduli spaces are algebraic varieties encoding the continuous parameters of linear algebra type classification problems. In recent years their topological and geometric properties have been explored, and applications to, among others, Donaldson-Thomas and Gromov-Witten theory have
From playlist Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum)

Introduction to Cylindrical Coordinates
Introduction to Cylindrical Coordinates Definition of a cylindrical coordinate and all of the formulas used to convert from cylindrical to rectangular and from rectangular to cylindrical. Examples are also given.
From playlist Calculus 3

"New Paradigms in Invariant Theory" - Roger Howe, Yale University [2011]
HKUST Institute for Advanced Study Distinguished Lecture New Paradigms in Invariant Theory Speaker: Prof Roger Howe, Yale University Date: 13/6/2011 Video taken from: http://video.ust.hk/Watch.aspx?Video=6A41D5F6B1A790DC
From playlist Mathematics

Vic Reiner, Lecture II - 11 February 2015
Vic Reiner (University of Minnesota) - Lecture II http://www.crm.sns.it/course/4036/ Many results in the combinatorics and invariant theory of reflection groups have q-analogues for the finite general linear groups GLn(Fq). These lectures will discuss several examples, and open questions
From playlist Algebraic topology, geometric and combinatorial group theory - 2015

Agnès David - Déformations galoisiennes et variétés de Kisin dans la conjecture de Breuil-Mézard
Je présenterai la structure de certains anneaux de déformations galoisiennes, dont l'étude est motivée par la conjecture de Breuil-Mézard. Celle-ci prédit des relations, régies par la correspondance de Langlands, entre les fibres spéciales de ces anneaux pour différentes contraintes de déf
From playlist The Paris-London Number Theory Seminar, Oct. 2019

Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum), Lecture 2
Quiver moduli spaces are algebraic varieties encoding the continuous parameters of linear algebra type classification problems. In recent years their topological and geometric properties have been explored, and applications to, among others, Donaldson-Thomas and Gromov-Witten theory have
From playlist Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum)

Nonlinear algebra, Lecture 10: "Invariant Theory", by Bernd Sturmfels
This is the tenth lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences.
From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

Anthony Henderson: Hilbert Schemes Lecture 4
SMRI Seminar Series: 'Hilbert Schemes' Lecture 4 Kleinian singularities 1 Anthony Henderson (University of Sydney) This series of lectures aims to present parts of Nakajima’s book `Lectures on Hilbert schemes of points on surfaces’ in a way that is accessible to PhD students interested i
From playlist SMRI Course: Hilbert Schemes

Markus Reineke - Cohomological Hall Algebras and Motivic Invariants for Quivers 1/4
We motivate, define and study Donaldson-Thomas invariants and Cohomological Hall algebras associated to quivers, relate them to the geometry of moduli spaces of quiver representations and (in special cases) to Gromov-Witten invariants, and discuss the algebraic structure of Cohomological H
From playlist 2021 IHES Summer School - Enumerative Geometry, Physics and Representation Theory

Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum), Lecture 4
Quiver moduli spaces are algebraic varieties encoding the continuous parameters of linear algebra type classification problems. In recent years their topological and geometric properties have been explored, and applications to, among others, Donaldson-Thomas and Gromov-Witten theory have
From playlist Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum)
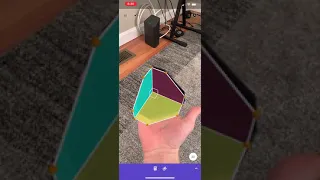
Octagonal Faced Protective Cover in GeoGebra 3D Calculator
It’s not an every-day occurrence to find 3 1/4-regular-octagons w/same center & where each is orthogonal to other 2 (packing material 🙂). Given (0,0,0) = center & side = 6.4, what are possible coordinate setups for other vertices? 🤔 #GeoGebra #3d #MTBoS #ITeachMath #math #maths
From playlist GeoGebra 3D with AR (iOS): Explorations, Demos, and Lesson Ideas

Introduction to Witt Vectors, delta-rings,and prisms (Lecture - 3) by James Broger
PERFECTOID SPACES ORGANIZERS: Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri, and Narasimha Kumar Cheraku DATE & TIME: 09 September 2019 to 20 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France) Eknath
From playlist Perfectoid Spaces 2019