
15.5: Lagrange Multipliers Example - Valuable Vector Calculus
Explanation of Lagrange multipliers: https://youtu.be/bmTiH4s_mYs An example of the actual problem-solving techniques to find maximum and minimum values of a function with a constraint using Lagrange multipliers. Full Valuable Vector Calculus playlist: https://www.youtube.com/playlist?li
From playlist Valuable Vector Calculus

Multimeter Review / DMM Review / buyers guide / tutorial
A list of my multimeters can be purchased here: http://astore.amazon.com/m0711-20?_encoding=UTF8&node=5 In this video I do a review of several digital multimeters. I compare features and functionality. I explain safety features, number of digits, display count, accuracy and resolution. Th
From playlist Multimeter reviews, buyers guide and comparisons.

Lagrange Multipliers: Relative Extrema of f=xy Under Constraint y=9-x^2
This video provides and example of how to use the method of Lagrange Multipliers.
From playlist Lagrange Multipliers

Lagrange Multipliers - Two Constraints
Thanks to all of you who support me on Patreon. You da real mvps! $1 per month helps!! :) https://www.patreon.com/patrickjmt !! Lagrange Multipliers - Two Constraints. In this video, I show how to find the maximum and minimum value of a function subject to TWO constraints using Lagrang
From playlist All Videos - Part 8
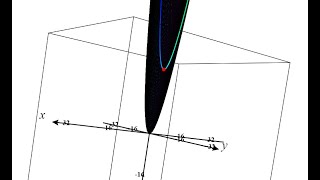
Lagrange Multipliers: Minimize f=x^2+y^2 under Constraint x+4y=20
This video provides and example of how to use the method of Lagrange Multipliers.
From playlist Lagrange Multipliers

Maximize a Function of Two Variable Under a Constraint Using Lagrange Multipliers
This video explains how to use Lagrange Multipliers to maximize a function under a given constraint. The results are shown in 3D.
From playlist Lagrange Multipliers

Bhargav Bhatt - The absolute prismatic site
Correction: The affiliation of Lei Fu is Tsinghua University. The absolute prismatic site of a p-adic formal scheme carries and organizes interesting arithmetic and geometric information attached to the formal scheme. In this talk, after recalling the definition of this site, I will discu
From playlist Conférence « Géométrie arithmétique en l’honneur de Luc Illusie » - 5 mai 2021

Lagrange Multipliers: Abs Extrema of Paraboloid Under Circular Constraint
This video provides and example of how to use the method of Lagrange Multipliers.
From playlist Lagrange Multipliers

Lagrange multipliers: 2 constraints
Free ebook http://tinyurl.com/EngMathYT A lecture showing how to apply the method of Lagrange multipliers where two contraints are involved.
From playlist Lagrange multipliers

Akhil Mathew - Remarks on p-adic logarithmic cohomology theories
Correction: The affiliation of Lei Fu is Tsinghua University. Many p-adic cohomology theories (e.g., de Rham, crystalline, prismatic) are known to have logarithmic analogs. I will explain how the theory of the “infinite root stack” (introduced by Talpo-Vistoli) gives an alternate approach
From playlist Conférence « Géométrie arithmétique en l’honneur de Luc Illusie » - 5 mai 2021

Lagrange Multipiers: Find the Max and Min of a Function of Two Variables
This video explains how to use Lagrange Multipliers to maximum and minimum a function under a given constraint. The results are shown in using level curves. http://mathispower4u.com
From playlist Lagrange Multipliers

Singularities in reductions of Shimura varieties -Thomas Haines
Joint IAS/Princeton University Number Theory Seminar Topic: Singularities in reductions of Shimura varieties Speaker: Thomas Haines Affiliation: University of Maryland Date: May 2, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

Schemes 37: Comparison of Weil and Cartier divisors
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. In this lecture we compare Cartier and Weil divisors, showing that for Noethernian integral schems the map from Cartier to Weil divisors is injective if the sc
From playlist Algebraic geometry II: Schemes

Schemes 36: Weil and Cartier divisors
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. In this lecture we define Weil and Cartier divisors and divisor classes, and give some simple examples of the groups of divisor classes.
From playlist Algebraic geometry II: Schemes

Schemes 39: Divisors and Dedekind domains
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. In this lecture we describe Weil and Cartier divisors for Dedekind domains, showing that they correspond to the two classical ways of defining the class group
From playlist Algebraic geometry II: Schemes

Akhil Mathew - Some recent advances in syntomic cohomology (3/3)
Bhatt-Morrow-Scholze have defined integral refinements $Z_p(i)$ of the syntomic cohomology of Fontaine-Messing and Kato. These objects arise as filtered Frobenius eigenspaces of absolute prismatic cohomology and should yield a theory of "p-adic étale motivic cohomology" -- for example, the
From playlist Franco-Asian Summer School on Arithmetic Geometry (CIRM)

Schemes 38: Comparison of Cartier divisors and Pic
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. In this lecture we Define a homomorphism from Caritier divisor classes to the Picard group, and show that it is an isomorphism for integral schemes. We use thi
From playlist Algebraic geometry II: Schemes

Uniformly valuative stability of polarized varieties and applications
Speaker: Yaxiong Liu (Tsinghua University) Abstract: In the study of K-stability, Fujita and Li proposed the valuative criterion of K-stability on Fano varieties, which has played an essential role of the algebraic theory of K-stability. Recently, Dervan-Legendre considered the valuative
From playlist Informal Geometric Analysis Seminar

Lagrange Multipliers Minimum of f(x, y, z) = x^2 + y^2 + z^2 subject to x + y + z - 9 = 0
Lagrange Multipliers Minimum of f(x, y, z) = x^2 + y^2 + z^2 subject to x + y + z - 9 = 0
From playlist Calculus 3

János Kollár - What determines a variety? - WAGON
A scheme X is a topological space---which we denote by |X|---and a sheaf of rings on the open subsets of |X|. We study the following natural but seldom considered questions. How to read off properties of X from |X|? Does |X| alone determine X? Joint work with Max Lieblich, Martin Olsson, a
From playlist WAGON