
The Two-Dimensional Discrete Fourier Transform
The two-dimensional discrete Fourier transform (DFT) is the natural extension of the one-dimensional DFT and describes two-dimensional signals like images as a weighted sum of two dimensional sinusoids. Two-dimensional sinusoids have a horizontal frequency component and a vertical frequen
From playlist Fourier

Math 139 Fourier Analysis Lecture 04: Uniqueness of Fourier Series
Uniqueness of Fourier Series: all Fourier coefficients vanish implies function vanishes at points of continuity; absolute convergence of Fourier series implies uniform convergence of Fourier series to the original (continuous) function; twice continuous differentiability implies absolute c
From playlist Course 8: Fourier Analysis

Intro to Fourier series and how to calculate them
Download the free PDF from http://tinyurl.com/EngMathYT This is a basic introduction to Fourier series and how to calculate them. An example is presented that illustrates the computations involved. Such ideas are seen in university mathematics.
From playlist Fourier

The Fourier Transform and Derivatives
This video describes how the Fourier Transform can be used to accurately and efficiently compute derivatives, with implications for the numerical solution of differential equations. Book Website: http://databookuw.com Book PDF: http://databookuw.com/databook.pdf These lectures follow
From playlist Fourier

The Discrete Fourier Transform
This video provides a basic introduction to the very widely used and important discrete Fourier transform (DFT). The DFT describes discrete-time signals as a weighted sum of complex sinusoid building blocks and is used in applications such as GPS, MP3, JPEG, and WiFi.
From playlist Fourier

The discrete-time Fourier transform
The Fourier transform is arguably the most important algorithm in signal processing and communications technology (not to mention neural time series data analysis!). This video provides an in-depth, step-by-step explanation of how the Fourier transform works. The video uses files you can
From playlist OLD ANTS #2) The discrete-time Fourier transform
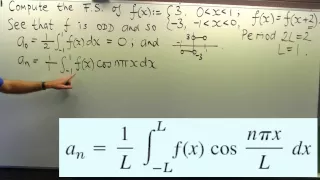
How to compute a Fourier series: an example
Free ebook http://tinyurl.com/EngMathYT This video is a demonstration on how to compute a Fourier series of a simple given function. I discuss how to calculate the Fourier coefficients through integration and the simplifications involved. Fourier series are an important area of applied
From playlist Engineering Mathematics

Math 139 Fourier Analysis Lecture 11.1: Fourier series need not converge at point of continuity
(Unfortunately I taped only part of this lecture.) Example of a function that is not the Fourier series of a Riemann integrable function. Beginning of the construction of a continuous function whose Fourier series diverges at a point (lecture stops at this point).
From playlist Course 8: Fourier Analysis

From playlist Coursera Regression V2

Intro to Fourier series & how to calculate them
Download the free PDF http://tinyurl.com/EngMathYT This is a basic introduction to Fourier series and how to calculate them. An example is presented that illustrates the computations involved. Such ideas are seen in university mathematics.
From playlist Several Variable Calculus / Vector Calculus

Nikos Sidiropoulos: "Supervised Learning and Canonical Decomposition of Multivariate Functions"
Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021 Workshop III: Mathematical Foundations and Algorithms for Tensor Computations "Supervised Learning and Canonical Decomposition of Multivariate Functions (Joint work with Nikos Kargas)" Nikos Sidiropoulos - Uni
From playlist Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021

Tutorial: Time Series Analysis - Matthew Graham - 6/24/2019
AstroInformatics 2019 Conference: Data Science and X-informatics http://astroinformatics2019.org/
From playlist AstroInformatics 2019 Conference

Data Driven Methods for Complex Turbulent Systems ( 3 ) - Andrew J. Majda
Lecture 3: Data Driven Methods for Complex Turbulent Systems Abstract: An important contemporary research topic is the development of physics constrained data driven methods for complex, large-dimensional turbulent systems such as the equations for climate change science. Three new approa
From playlist Mathematical Perspectives on Clouds, Climate, and Tropical Meteorology

The Discrete Fourier Transform: Sampling the DTFT
http://AllSignalProcessing.com for free e-book on frequency relationships and more great signal processing content, including concept/screenshot files, quizzes, MATLAB and data files.
From playlist Fourier

Stéphane Jaffard - Conférence organisée par l'Institut Fourier et le Laboratoire Jean Kuntzmann
Conférence organisée par l'Institut Fourier et le Laboratoire Jean Kuntzmann Licence: CC BY NC-ND 4.0
From playlist Conférences grand public "MathEnVille"

The perfection of the Fourier transform
This video lesson is part of a complete course on neuroscience time series analyses. The full course includes - over 47 hours of video instruction - lots and lots of MATLAB exercises and problem sets - access to a dedicated Q&A forum. You can find out more here: https://www.udemy.
From playlist NEW ANTS #2) Static spectral analysis

Steve Brunton: "Dynamical Systems (Part 2/2)"
Watch part 1/2 here: https://youtu.be/2VBN_dJZLWc Machine Learning for Physics and the Physics of Learning Tutorials 2019 "Dynamical Systems (Part 2/2)" Steve Brunton, University of Washington Institute for Pure and Applied Mathematics, UCLA September 6, 2019 For more information: http
From playlist Machine Learning for Physics and the Physics of Learning 2019

Lec 24 | MIT 18.085 Computational Science and Engineering I
Discrete filters: lowpass and highpass A more recent version of this course is available at: http://ocw.mit.edu/18-085f08 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 18.085 Computational Science & Engineering I, Fall 2007

Structured Regularization Summer School - L. Rosasco - 2/4 - 21/06/2017
Lorenzo Rosasco (Genova and MIT): Regularization Methods for Large Scale Machine Learning Abstract: Regularization techniques originally developed to solve linear inverse problems can be extended to derive nonparametric machine learning methods. These methods perform well in practice and
From playlist Structured Regularization Summer School - 19-22/06/2017
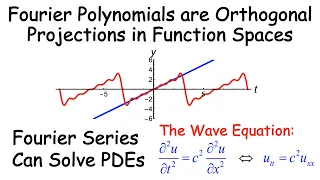
Fourier Series (for PDEs) w/ Fourier Polynomials (Orthogonal Projections in Inner Product Spaces)
Fourier Series (for Partial Differential Equations) are Constructed with Fourier Polynomials, which are Orthogonal Projections in Inner Product Spaces (in this case, the Function Space of Real-Valued Continuous Functions C[-pi,pi] with the inner product of f and g defined to be the integra
From playlist Fourier