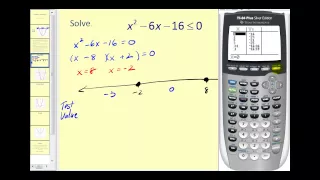
Solving Quadratic Inequalities
This video explains how to solve quadratic inequalities algebraically and graphically. http://mathispower4u.wordpress.com/
From playlist Quadratic Functions and Equations

Hyperbolic trigonometric functions
Definition of the hyperbolic sine and cosine functions from solving second-order differential equation. Join me on Coursera: Matrix Algebra for Engineers: https://www.coursera.org/learn/matrix-algebra-engineers Differential Equations for Engineers: https://www.coursera.org/learn/differe
From playlist Differential Equations
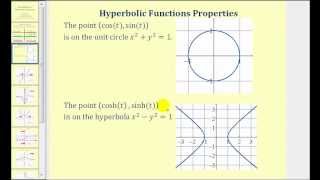
Introduction to Hyperbolic Functions
This video provides a basic overview of hyperbolic function. The lesson defines the hyperbolic functions, shows the graphs of the hyperbolic functions, and gives the properties of hyperbolic functions. Site: http://mathispower4u.com Blog: http://mathispower4u.wordpress.com
From playlist Differentiation of Hyperbolic Functions

(ML 19.5) Positive semidefinite kernels (Covariance functions)
Definition of a positive semidefinite kernel, or covariance function. A simple example. Explanation of terminology: autocovariance, positive definite kernel, stationary kernel, isotropic kernel, covariogram, positive definite function.
From playlist Machine Learning

This video explains how to final the axis of symmetry, vertex, and intercepts of a quadratic function. It also shows how to graph the function, determine the domain and range, as well as the intervals for which the function is increasing and decreasing. Site: http://mathispower4u.com
From playlist Graphing Quadratic Functions

Seminar on Applied Geometry and Algebra (SIAM SAGA): Bernd Sturmfels
Date: Tuesday, February 9 at 11:00am EST (5:00pm CET) Speaker: Bernd Sturmfels, MPI MiS Leipzig / UC Berkeley Title: Linear Spaces of Symmetric Matrices. Abstract: Real symmetric matrices appear ubiquitously across the mathematical sciences, and so do linear spaces of such matrices. We
From playlist Seminar on Applied Geometry and Algebra (SIAM SAGA)
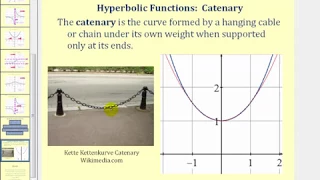
Introduction to Hyperbolic Functions
This video provides a basic overview of hyperbolic function. The lesson defines the hyperbolic functions, shows the graphs of the hyperbolic functions, and gives the properties of hyperbolic functions.
From playlist Using the Properties of Hyperbolic Functions

Rick Kenyon - The multinomial Ising model
The multinomial Ising model on a graph $G=(V,E)$ is the Ising model on the N-fold “blow-up” $G_N$ of $G$, whose vertices are $V\times[N]$, and edges connect $(u,i)$ to $(v,j)$ iff $u$ and $v$ are adjacent. In the limit of large $N$ we find the critical temperature, phase transitions,
From playlist 100…(102!) Years of the Ising Model

http://mathispower4u.wordpress.com/
From playlist Quadratic Functions and Equations

“The Automatic Statistician”– Professor Zoubin Ghahramani
Talk given by Professor of Information Engineering at the University of Cambridge, leader of the Cambridge Machine Learning Group, and the Cambridge Liaison Director of the Alan Turing Institute; Zoubin Ghahramani. The lecture regards the use of Bayesian model selection strategies that aut
From playlist Turing Seminars

ML Tutorial: Bayesian Machine Learning (Zoubin Ghahramani)
Machine Learning Tutorial at Imperial College London: Bayesian Machine Learning Zoubin Ghahramani (University of Cambridge) January 29, 2014
From playlist Machine Learning Tutorials

E-commerce Anomaly Detection: A Bayesian Semi-Supervised Tensor.... by Anil Yelundur
DISCUSSION MEETING THE THEORETICAL BASIS OF MACHINE LEARNING (ML) ORGANIZERS: Chiranjib Bhattacharya, Sunita Sarawagi, Ravi Sundaram and SVN Vishwanathan DATE : 27 December 2018 to 29 December 2018 VENUE : Ramanujan Lecture Hall, ICTS, Bangalore ML (Machine Learning) has enjoyed tr
From playlist The Theoretical Basis of Machine Learning 2018 (ML)
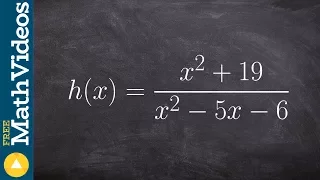
Determine the domain of a rational function by factoring the denominator
👉 Learn how to find the domain of rational functions. Recall that the domain of a function is the set of possible input values (x-values) of the function. For a rational function, the denominator cannot be zero. Thus, to find the domain of a rational function, we first find the values of x
From playlist Domain of a function with a fraction | Quadratic

Marcus Appleby: Number theoretic features of a SIC
Marcus Appleby: Number theoretic features of a SIC Abstract: The lecture was held within the framework of the Hausdorff Trimester Program Mathematics of Signal Processing. The problem of proving, or disproving SIC existence (i.e. maximal sets of equiangular lines in Cd, or symmetric info
From playlist HIM Lectures: Trimester Program "Mathematics of Signal Processing"

Alisa Knizel: Log-gases on a quadratic lattice via discrete loop equations
We study a general class of log-gas ensembles on a quadratic lattice. Using a variational principle we prove that the corresponding empirical measures satisfy a law of large numbers and that their global fluctuations are Gaussian with a universal covariance. We apply our general results to
From playlist Jean-Morlet Chair - Grava/Bufetov
Branimir Cacic, Classical gauge theory on quantum principalbundles
Noncommutative Geometry Seminar (Europe), 20 October 2021
From playlist Global Noncommutative Geometry Seminar (Europe)

Domain of a rational function by factoring
👉 Learn how to find the domain of rational functions. Recall that the domain of a function is the set of possible input values (x-values) of the function. For a rational function, the denominator cannot be zero. Thus, to find the domain of a rational function, we first find the values of x
From playlist Domain of a function with a fraction | Quadratic

Pieter Blue - Decay for fields outside black holes
I will discuss energy and Morawetz (or integrated local decay) estimates for fields outside black holes. These results build on results for the wave equation and use the Killing tensor, an unusual geometric object that exists in the Kerr spacetime.
From playlist Ecole d'été 2014 - Analyse asymptotique en relativité générale
ML Tutorial: Gaussian Processes (Richard Turner)
Machine Learning Tutorial at Imperial College London: Gaussian Processes Richard Turner (University of Cambridge) November 23, 2016
From playlist Machine Learning Tutorials
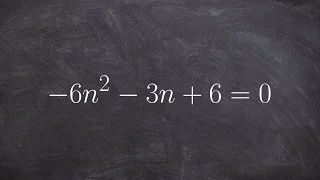
How to use the discriminat to describe your solutions
👉 Learn how to determine the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. T
From playlist Discriminant of a Quadratic Equation