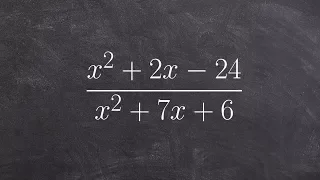
Simplify a rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions
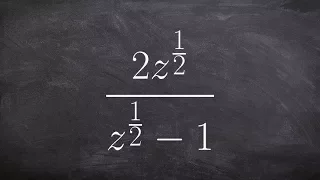
Learn how to rationalize the denominator with a rational exponent
👉 Learn how to rationalize the denominator. Rationalization is the simplification of a rational expression by multiplying the denominator and the numerator of the expression by the conjugate of the denominator. The conjugate of an expression of two terms is obtained by changing the sign be
From playlist Rationalize the Denominator with Fractional Exponent

Learning to simplify a rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions
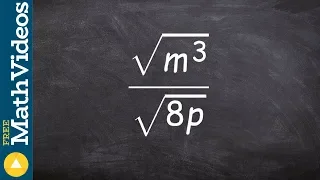
Learn to rationalize the denominator with a monomial as the denominator ex 6
👉 Learn how to rationalize the denominator. Rationalization is the simplification of a rational expression by multiplying the denominator and the numerator of the expression by the conjugate of the denominator. The conjugate of an expression of two terms is obtained by changing the sign be
From playlist Rationalize the Denominator with Fractional Exponent
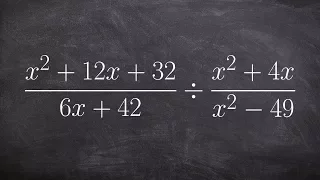
Learn how to divide rational expressions. A rational expression is an expression in the form of a fraction, usually having variable(s) in the denominator. Recall that to divide by a fraction, we multiply by the reciprocal of the fraction. The same rule applies when we want to divide by a r
From playlist How to Divide Rational Expressions #Rational

Learn how to divide rational expressions. A rational expression is an expression in the form of a fraction, usually having variable(s) in the denominator. Recall that to divide by a fraction, we multiply by the reciprocal of the fraction. The same rule applies when we want to divide by a r
From playlist How to Divide Rational Expressions #Rational

Dividing two rational expressions by factoring
Learn how to divide rational expressions. A rational expression is an expression in the form of a fraction, usually having variable(s) in the denominator. Recall that to divide by a fraction, we multiply by the reciprocal of the fraction. The same rule applies when we want to divide by a r
From playlist How to Divide Rational Expressions #Rational

In this video we cover some rational function fundamentals, including asymptotes and interecepts.
From playlist Polynomial Functions
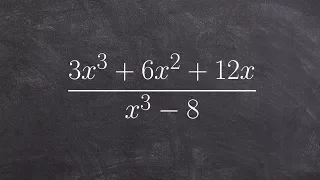
Simplify a rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions
algebraic geometry 31 Rational maps
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers the definition of rational functions and rational maps, and gives an example of a cubic curve that is not birational to the affine line.
From playlist Algebraic geometry I: Varieties

Set Theory (Part 18): The Rational Numbers are Countably Infinite
Please feel free to leave comments/questions on the video and practice problems below! In this video, we will show that the rational numbers are equinumerous to the the natural numbers and integers. First, we will go over the standard argument listing out the rational numbers in a table a
From playlist Set Theory by Mathoma

Higher Algebra 11: p-adic completion (corrected)
In this video we introduce the notion of p-adic completion and p-adic equivalence of spectra. We characterize those notions in concrete terms and give examples. Finally we cover the Hasse-square, which can be used to recover X from it completions and its rationalisation. All the material i
From playlist Higher Algebra

Sabyasachi Mukherjee: Interbreeding in conformal dynamics, and its applications near and far
HYBRID EVENT Recorded during the meeting "Advancing Bridges in Complex Dynamics" the September 24, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM
From playlist Virtual Conference

Rational Homotopy Groups (Lecture 3) By Somnath Basu
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)

Massimiliano Mella: Unirational varieties - Part 1
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Finding rational curves by forgetful map - Runpu Zong
Runpu Zong Member, School of Mathematics October 1, 2014 More videos on http://video.ias.edu
From playlist Mathematics

Factoring out the GCF to simplify the rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions (Binomials) #Rational


