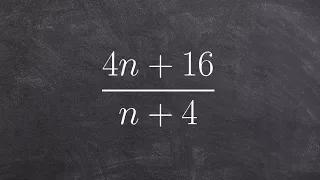
Simplifying rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions (Binomials) #Rational

Simplifying a rational expression by factoring
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions
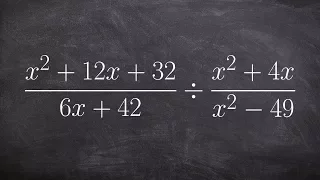
Learn how to divide rational expressions. A rational expression is an expression in the form of a fraction, usually having variable(s) in the denominator. Recall that to divide by a fraction, we multiply by the reciprocal of the fraction. The same rule applies when we want to divide by a r
From playlist How to Divide Rational Expressions #Rational

Divide two rational expressions by simplifying
Learn how to divide rational expressions. A rational expression is an expression in the form of a fraction, usually having variable(s) in the denominator. Recall that to divide by a fraction, we multiply by the reciprocal of the fraction. The same rule applies when we want to divide by a r
From playlist How to Divide Rational Expressions #Rational

Simplify a rational expression by factoring trinomials
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions

Simplify a rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions (Binomials) #Rational

Simplifying a rational expression with rational exponents
👉 Learn how to divide with rational powers. To divide with numbers/expressions with rational exponents, we apply the basic rules of exponents. If the two numbers/expressions are the same, we simply take one of the number and raise it to the power of the difference between the exponents of
From playlist Divide Rational Exponents

Solving a rational equation when the LCD is a binomial expression
👉 Learn how to solve rational equations. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. There are many ways to solve rational equations, one of the ways is by multiplying all the individual rationa
From playlist How to Solve Rational Equations with an Integer

Set Theory (Part 13): Constructing the Rational Numbers
Please feel free to leave comments/questions on the video and practice problems below! In this video, we will use the integers to construct the rational numbers as a quotient set, just as we constructed the integers. We will also introduce arithmetic on the rational numbers and show that
From playlist Set Theory by Mathoma

Choice Functions and Length: Why you can't measure everything you choose
I haven't talked about the axiom of choice in a while, and the relationship between choice functions and length (or size) and why you can't measure everything you choose seemed like a good way to do so. The interplay between choice functions and how one can construct sets for which measure
From playlist The New CHALKboard

Nick Addington - Rational points and derived equivalence - WAGON
For smooth projective varieties over Q, is the existence of a rational point preserved under derived equivalence? First I'll discuss why this question is interesting, and what is known. Then I'll show that the answer is no, giving two counterexamples: an abelian variety and a torsor over i
From playlist WAGON

Marcello Bernardara: Semiorthogonal decompositions and birational geometry of geometrically rational
Abstract:This is a joint work in progress with A. Auel. Let S be a geometrically rational del Pezzo surface over a field k. In this talk, I will show how the k-rationality of S is equivalent to the existence of some semiorthogonal decompositions of its derived category. In particular, the
From playlist HIM Lectures: Junior Trimester Program "Algebraic Geometry"

Set Theory (Part 16): Correspondence Between Number Systems
Please feel free to leave comments/questions on the video and practice problems below! In this video, we will connect the number systems together through isomorphic embedding functions, so that operations are preserved across number systems. I will also argue that, in the strict sense, th
From playlist Set Theory by Mathoma

Higher Algebra 11: p-adic completion (corrected)
In this video we introduce the notion of p-adic completion and p-adic equivalence of spectra. We characterize those notions in concrete terms and give examples. Finally we cover the Hasse-square, which can be used to recover X from it completions and its rationalisation. All the material i
From playlist Higher Algebra

How to use the LCD to help us solve a rational equation
👉 Learn how to solve proportions. Two ratios are said to be proportional when the two ratios are equal. Thus, proportion problems are problems involving the equality of two ratios. When given a proportion problem with an unknown, we usually cross-multiply the two ratios and then solve for
From playlist How to Solve Rational Equations

Massimiliano Mella: Unirational varieties - Part 1
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Jacob Lurie: 1/5 Tamagawa numbers in the function field case [2019]
Slides for this talk: http://swc-alpha.math.arizona.edu/video/2019/2019LurieLecture1Slides.pdf Lecture notes: http://swc.math.arizona.edu/aws/2019/2019LurieNotes.pdf Let G be a semisimple algebraic group defined over the field Q of rational numbers and let G(Q) denote the group of ration
From playlist Number Theory

Finite or infinite? One key to algebraic cycles - Burt Totaro
Burt Totaro University of California, Los Angeles; Member, School of Mathematics February 2, 2015 Algebraic cycles are linear combinations of algebraic subvarieties of an algebraic variety. We want to know whether all algebraic subvarieties can be built from finitely many, in a suitable s
From playlist Mathematics

Simplifying a rational expression using rational exponents
👉 Learn how to divide with rational powers. To divide with numbers/expressions with rational exponents, we apply the basic rules of exponents. If the two numbers/expressions are the same, we simply take one of the number and raise it to the power of the difference between the exponents of
From playlist Divide Rational Exponents
