
Ramanujan: Making sense of 1+2+3+... = -1/12 and Co.
The Mathologer sets out to make sense of 1+2+3+ ... = -1/12 and some of those other notorious, crazy-looking infinite sum identities. The starting point for this video is the famous letter that led to the discovery of self-taught mathematical genius Srinivasa Ramanujan in 1913 (Ramanujan i
From playlist Recent videos

What is Hardy Ramanujan Number? || #YTShorts || Don't Memorise
Ramanujan was fascinated with numbers and made striking contributions to the branch of mathematics. One of which is the Hardy-Ramanujan number. Want to know what this number is? Watch this video- Don’t Memorise brings learning to life through its captivating educational videos. To Know Mo
From playlist Shorts

History of Indian Mathematics Part V: Ramanujan's Discoveries
Learn about Srinivasa Ramanujan, one of history's greatest mathematical minds! Check out the whole series on the blog: https://centerofmathematics.blogspot.com/2019/11/history-of-indian-mathematics.html
From playlist History of Indian Mathematics

The third video in a series about Ramanujan.This one is about Ramanujan Summation. Here's the wikipedia page for further reading: https://en.wikipedia.org/wiki/Ramanujan_summation Euler-Maclaurin Formula https://en.wikipedia.org/wiki/Euler%E2%80%93Maclaurin_formula --------- Here is a
From playlist My Maths Videos

In this video, I evaluate the integral from 0 to infinity of e^(-x^3) sin(x^3) dx using a very nice formula due to Ramanujan, which relates integrals of the form x^s f(x) with a sort of power series of f. Enjoy! Note: I would like to thank philosophicalmath for this idea, you should check
From playlist Integrals

The second video in a series about Ramanujan. Continuing the biography and a look at another of Ramanujan's formulas. This one involves Ramanujan's pi formula.
From playlist My Maths Videos

Ramanujan's infinite root and its crazy cousins
In this video I'll talk about Ramanujan's infinite roots problem, give the solution to my infinite continued fraction puzzle from a couple of week's ago, and let you in on the tricks of the trade when it comes to making sense of all those crazy infinite expressions. Featuring guest appeara
From playlist Recent videos
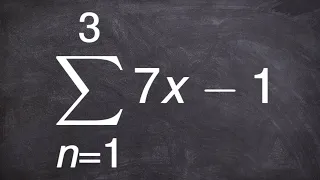
Finding the sum or an arithmetic series using summation notation
👉 Learn how to find the partial sum of an arithmetic series. A series is the sum of the terms of a sequence. An arithmetic series is the sum of the terms of an arithmetic sequence. The formula for the sum of n terms of an arithmetic sequence is given by Sn = n/2 [2a + (n - 1)d], where a is
From playlist Series

The Ramanujan Conjecture and some diophantine equations - Peter Sarnak
Speaker : Peter Sarnak Date and Time : Faculty Hall, IISc, Bangalore Venue : 25 May 12, 16:00 One of Ramanujan's most influential conjectures concerns the magnitude of the Fourier Coefficients of a modular form. These were made on the basis of his calculations as well as a far-reaching in
From playlist Public Lectures

Indian Literature: The Ramayana | The Great Courses Plus
It's a 24,000-verse poem with a ten-headed demon—and widely accepted as fact. The Ramayana is an ancient epic of historic Indian literature, but also a religious text for the Hindu. Pack your bags and join Prince Rama and his wife, Sita, on their exile in the forest and the trials they fac
From playlist World History

How did Ramanujan solve the STRAND puzzle?
Today's video is about making sense of an infinite fraction that pops up in an anecdote about the mathematical genius Srinivasa Ramanujan. 00:00 Intro 04:31 Chapter 1: Getting a feel for the puzzle 08:27 Chapter 2: Algebra autopilot 12:37 Chapter 3: Infinite fraction 17:51 Chapter 4: Roo
From playlist Recent videos
Can p-adic integrals be computed? - William Duke
Automorphic Forms William Duke Thomas Hales April 6, 2001 Concepts, Techniques, Applications and Influence April 4, 2001 - April 7, 2001 Support for this conference was provided by the National Science Foundation Conference Page: https://www.math.ias.edu/conf-automorphicforms Confere
From playlist Mathematics

Number Theory, Symmetry and Zeta Functions - Peter Sarnak
75th Anniversary Celebration School of Mathematics Peter Sarnak Institute for Advanced Study March 11, 2005 More videos on http://video.ias.edu
From playlist Mathematics

The finite part of infinity (ONLINE) by Joseph Samuel
Vigyan Adda The finite part of infinity (ONLINE) Speaker: Joseph Samuel (RRI & ICTS-TIFR, Bengaluru) When: 4:30 pm to 6:00 pm Sunday, 24 October 2021 Where: Livestream via the ICTS YouTube channel Abstract: - Ramanujan's notebooks contain the equation 1+2+3....= - 1/12. While this see
From playlist Vigyan Adda

Laurent Massoulié : Non-backtracking spectrum of random graphs: community detection and ...
Abstract: A non-backtracking walk on a graph is a directed path such that no edge is the inverse of its preceding edge. The non-backtracking matrix of a graph is indexed by its directed edges and can be used to count non-backtracking walks of a given length. It has been used recently in th
From playlist Combinatorics
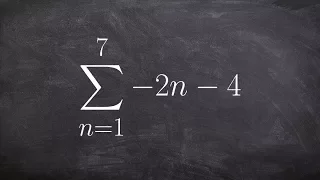
Learn to use summation notation for an arithmetic series to find the sum
👉 Learn how to find the partial sum of an arithmetic series. A series is the sum of the terms of a sequence. An arithmetic series is the sum of the terms of an arithmetic sequence. The formula for the sum of n terms of an arithmetic sequence is given by Sn = n/2 [2a + (n - 1)d], where a is
From playlist Series