
A short refresher on vectors. Before I introduce vector-based functions, it's important to look at vectors themselves and how they are represented in python™ and the IPython Notebook using SymPy.
From playlist Life Science Math: Vectors

(New Version Available) Inverse Functions
New Version: https://youtu.be/q6y0ToEhT1E Define an inverse function. Determine if a function as an inverse function. Determine inverse functions. http://mathispower4u.wordpress.com/
From playlist Exponential and Logarithmic Expressions and Equations
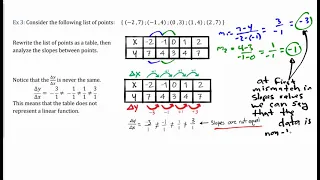
Define linear functions. Use function notation to evaluate linear functions. Learn to identify linear function from data, graphs, and equations.
From playlist Algebra 1

Transcendental Functions 19 The Function a to the power x.mp4
The function a to the power x.
From playlist Transcendental Functions

Transcendental Functions 3 Examples using Properties of Logarithms.mov
Examples using the properties of logarithms.
From playlist Transcendental Functions

Transcendental Functions 11 Inverse Functions Part 1.mov
Moving on in our study of transcendental functions, we look at the inverse of a function.
From playlist Transcendental Functions

Lec 8 | MIT 5.112 Principles of Chemical Science, Fall 2005
P Orbitals View the complete course: http://ocw.mit.edu/5-112F05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 5.112 Principles of Chemical Science, Fall 2005

Lec 8 | MIT 5.111 Principles of Chemical Science, Fall 2005
P Orbitals (Prof. Sylvia Ceyer) View the complete course: http://ocw.mit.edu/5-111F05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 5.111 Principles of Chemical Science, Fall 2005

Define an inverse function. Determine if a function as an inverse function. Determine inverse functions.
From playlist Determining Inverse Functions

Transcendental Functions 13 Derivatives of a Function and its Inverse.mov
The first derivative of a function and the inverse of that function.
From playlist Transcendental Functions

Define a linear function. Determine if a linear function is increasing or decreasing. Interpret linear function models. Determine linear functions. Site: http://mathispower4u.com
From playlist Introduction to Functions: Function Basics

Jacek Dziubański: Selected results in real harmonic analysis in the rational Dunkl setting
HYBRID EVENT Recorded during the meeting "Modern Analysis Related to Root Systems with Applications" the October 19, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathe
From playlist Virtual Conference

6. Hydrogen Atom Wavefunctions (Orbitals)
MIT 5.111 Principles of Chemical Science, Fall 2014 View the complete course: https://ocw.mit.edu/5-111F14 Instructor: Catherine Drennan Where is that electron anyway? In this lecture, the probability of finding an electron at a particular distance from the nucleus is discussed. The conce
From playlist MIT 5.111 Principles of Chemical Science, Fall 2014

Lecture 27 | The Fourier Transforms and its Applications
Lecture by Professor Brad Osgood for the Electrical Engineering course, The Fourier Transforms and its Applications (EE 261). Professor Osgood continues his discussion on higher dimensions and the outer reaches while helping the students understand higher dimensions Fourier Transforms.
From playlist Lecture Collection | The Fourier Transforms and Its Applications

Lec 7 | MIT 5.112 Principles of Chemical Science, Fall 2005
Hydrogen Atom Wave functions View the complete course: http://ocw.mit.edu/5-112F05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 5.112 Principles of Chemical Science, Fall 2005

Virginie Ehrlacher - Multi-center decomposition of molecular densities: a mathematical perspective
Recorded 04 May 2022. Virginie Ehrlacher of the École Nationale des Ponts-et-Chaussées presents "Multi-center decomposition of molecular densities: a mathematical perspective" at IPAM's Large-Scale Certified Numerical Methods in Quantum Mechanics Workshop. Abstract: The aim of this talk is
From playlist 2022 Large-Scale Certified Numerical Methods in Quantum Mechanics

MIT 5.111 Principles of Chemical Science, Fall 2008 View the complete course: http://ocw.mit.edu/5-111F08 Instructor: Catherine Drennan, Elizabeth Vogel Taylor License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 5.111 Principles of Chemical Science, Fall 2008

Radial Basis Function Networks are not talked about a lot these days, but they are very interesting and useful. Handwriting demo: http://macheads101.com/demos/handwriting/?c=rbf Resizing images with RBF networks: https://github.com/unixpickle/rbfscale#results Distance formula in kNN vid
From playlist Machine Learning
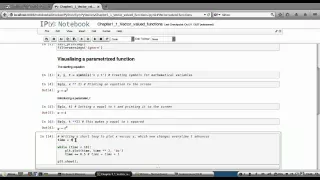
Now that we had a quick refresher on vectors, let's look at what constitutes a vector-valued function. In this lecture I use python code to illustrate these functions.
From playlist Life Science Math: Vectors

Lecture 04-Jack Simons Electronic Structure Theory- Linear combinations of atomic orbitals
The Hartree-Fock molecular orbitals; LCAO-MO expansion; Hartree-Fock equations in matrix form; one- and two-electron integrals; the iterative SCF process; scaling with basis set size; how virtual orbitals change with basis set; core, valence, polarization, and diffuse basis functions; Slat
From playlist U of Utah: Jack Simons' Electronic Structure Theory course