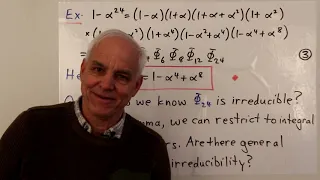
Irreducibility and the Schoenemann-Eisenstein criterion | Famous Math Probs 20b | N J Wildberger
In the context of defining and computing the cyclotomic polynumbers (or polynomials), we consider irreducibility. Gauss's lemma connects irreducibility over the integers to irreducibility over the rational numbers. Then we describe T. Schoenemann's irreducibility criterion, which uses some
From playlist Famous Math Problems

CurvesSurfaces3: De Casteljau Bezier Curves in Algebraic Calculus | N J Wildberger
We explain how to extend Archimedes' famous Parabolic Area Formula to the cubic situation. This formula was historically the first major calculation in Calculus, and gave an explicit and workable formula for the area of a slice of a parabola, cut off by a chord, in terms of the area of a p
From playlist MathSeminars

Theory of numbers: Gauss's lemma
This lecture is part of an online undergraduate course on the theory of numbers. We describe Gauss's lemma which gives a useful criterion for whether a number n is a quadratic residue of a prime p. We work it out explicitly for n = -1, 2 and 3, and as an application prove some cases of Di
From playlist Theory of numbers

Proof & Explanation: Gauss's Lemma in Number Theory
Euler's criterion: https://youtu.be/2IBPOI43jek One common proof of quadratic reciprocity uses Gauss's lemma. To understand Gauss's lemma, here we prove how it works using Euler's criterion and the Legendre symbol. Quadratic Residues playlist: https://www.youtube.com/playlist?list=PLug5Z
From playlist Quadratic Residues

On the structure of measures constrained by linear PDEs – Guido De Philippis – ICM2018
Partial Differential Equations | Analysis and Operator Algebras Invited Lecture 10.3 | 8.3 On the structure of measures constrained by linear PDEs Guido De Philippis Abstract: The aim of this talk is to present some recent results on the structure of the singular part of measures satisfy
From playlist Partial Differential Equations

Niebur Integrals and Mock Automorphic Forms - Wladimir de Azevedo Pribitkin
Wladimir de Azevedo Pribitkin College of Staten Island, CUNY March 17, 2011 Among the bounty of brilliancies bequeathed to humanity by Srinivasa Ramanujan, the circle method and the notion of mock theta functions strike wonder and spark intrigue in number theorists fresh and seasoned alike
From playlist Mathematics

Scott Ahlgren: Algebraic and transcendental formulas for the smallest parts function
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Number Theory

Adam Oberman: "Generalization Theory in Machine Learning" (Part 1/2)
Watch part 2/2 here: https://youtu.be/uFyb_IHTiN8 High Dimensional Hamilton-Jacobi PDEs Tutorials 2020 "Generalization Theory in Machine Learning" (Part 1/2) Adam Oberman, McGill University Abstract: Statistical learning theory addresses the following question. Given a sample of data po
From playlist High Dimensional Hamilton-Jacobi PDEs 2020

D. Vittone - Rectifiability issues in sub-Riemannian geometry
In this talk we discuss two problems concerning “rectifiability” in sub-Riemannian geometry and particularly in the model setting of Carnot groups. The first problem regards the rectifiability of boundaries of sets with finite perimeter in Carnot groups, while the second one concerns Radem
From playlist Journées Sous-Riemanniennes 2018
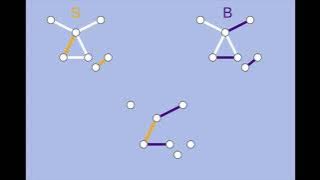
Berge's lemma, an animated proof
Berge's lemma is a mathematical theorem in graph theory which states that a matching in a graph is of maximum cardinality if and only if it has no augmenting paths. But what do those terms even mean? And how do we prove Berge's lemma to be true? == CORRECTION: at 7:50, the red text should
From playlist Summer of Math Exposition Youtube Videos

What Do We Know About Matrix Estimation? (Lecture 3) by Devavrat Shah
PROGRAM : ADVANCES IN APPLIED PROBABILITY ORGANIZERS : Vivek Borkar, Sandeep Juneja, Kavita Ramanan, Devavrat Shah and Piyush Srivastava DATE & TIME : 05 August 2019 to 17 August 2019 VENUE : Ramanujan Lecture Hall, ICTS Bangalore Applied probability has seen a revolutionary growth in r
From playlist Advances in Applied Probability 2019

Large Deviations for the Largest Eigenvalue of Sub-Gaussian Wigner Matrices by Nicholas Cook
PROGRAM: TOPICS IN HIGH DIMENSIONAL PROBABILITY ORGANIZERS: Anirban Basak (ICTS-TIFR, India) and Riddhipratim Basu (ICTS-TIFR, India) DATE & TIME: 02 January 2023 to 13 January 2023 VENUE: Ramanujan Lecture Hall This program will focus on several interconnected themes in modern probab
From playlist TOPICS IN HIGH DIMENSIONAL PROBABILITY

Hard Lefschetz Theorem and Hodge-Riemann Relations for Combinatorial Geometries - June Huh
June Huh Princeton University; Veblen Fellow, School of Mathematics November 9, 2015 https://www.math.ias.edu/seminars/abstract?event=47563 A conjecture of Read predicts that the coefficients of the chromatic polynomial of a graph form a log-concave sequence for any graph. A related conj
From playlist Members Seminar

Introduction to additive combinatorics lecture 1.8 --- Plünnecke's theorem
In this video I present a proof of Plünnecke's theorem due to George Petridis, which also uses some arguments of Imre Ruzsa. Plünnecke's theorem is a very useful tool in additive combinatorics, which implies that if A is a set of integers such that |A+A| is at most C|A|, then for any pair
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Cayley-Hamilton Theorem Example 2
Matrix Theory: Let A be the 3x3 matrix A = [1 2 2 / 2 0 1 / 1 3 4] with entries in the field Z/5. We verify the Cayley-Hamilton Theorem for A and compute the inverse of I + A using a geometric power series.
From playlist Matrix Theory

Nick Cook (Duke) -- Universality for the minimum modulus of random trigonometric polynomials
We consider the restriction to the unit circle of random degree-n polynomials with iid normalized coefficients (Kac polynomials). Recent work of Yakir and Zeitouni shows that for Gaussian coefficients, the minimum modulus (suitably rescaled) follows a limiting exponential distribution. We
From playlist Columbia Probability Seminar

What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics

Tensor Decomposition Definitions of Neural Net Architectures
This paper describes complexity theory of neural networks, defined by tensor decompositions, with a review of simplification of the tensor decomposition for simpler neural network architectures. The concept of Z-completeness for a network N is defined in the existence of a tensor decomposi
From playlist Wolfram Technology Conference 2021

William B. Johnson: Ideals in L(L_p)
Abstract: I’ll discuss the Banach algebra structure of the spaces of bounded linear operators on ℓp and Lp := Lp(0,1). The main new results are 1. The only non trivial closed ideal in L(Lp), 1 ≤ p [is less than] ∞, that has a left approximate identity is the ideal of compact operators (joi
From playlist Analysis and its Applications

Applying reimann sum for the midpoint rule and 3 partitions
👉 Learn how to approximate the integral of a function using the Reimann sum approximation. Reimann sum is an approximation of the area under a curve or between two curves by dividing it into multiple simple shapes like rectangles and trapezoids. In using the Reimann sum to approximate the
From playlist The Integral