This video explains what information the gradient provides about a given function. http://mathispower4u.wordpress.com/
From playlist Functions of Several Variables - Calculus

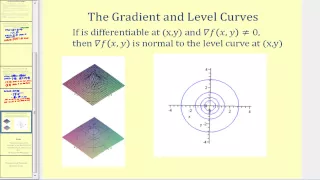
11_3_1 The Gradient of a Multivariable Function
Using the partial derivatives of a multivariable function to construct its gradient vector.
From playlist Advanced Calculus / Multivariable Calculus

Introduction to the Gradient Theory and Formulas
Introduction to the Gradient Theory and Formulas If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)
From playlist Calculus 3

Lieven Vandenberghe: "Bregman proximal methods for semidefinite optimization."
Intersections between Control, Learning and Optimization 2020 "Bregman proximal methods for semidefinite optimization." Lieven Vandenberghe - University of California, Los Angeles (UCLA) Abstract: We discuss first-order methods for semidefinite optimization, based on non-Euclidean projec
From playlist Intersections between Control, Learning and Optimization 2020

Suvrit Sra: Lecture series on Aspects of Convex, Nonconvex, and Geometric Optimization (Lecture 2)
The lecture was held within the framework of the Hausdorff Trimester Program "Mathematics of Signal Processing". (26.1.2016)
From playlist HIM Lectures: Trimester Program "Mathematics of Signal Processing"

Find the Gradient Vector Field of f(x,y)=ln(2x+5y)
This video explains how to find the gradient of a function. It also explains what the gradient tells us about the function. The gradient is also shown graphically. http://mathispower4u.com
From playlist The Chain Rule and Directional Derivatives, and the Gradient of Functions of Two Variables

Can You Do ADVANCED Calculus?!?
How To Calculate The Gradient Vector In Calculus 3!! #Calculus #Multivariable #Math #Gradient #NicholasGKK #Shorts
From playlist Calculus
Find the Gradient Vector Field of f(x,y)=x^3y^5
This video explains how to find the gradient of a function. It also explains what the gradient tells us about the function. The gradient is also shown graphically. http://mathispower4u.com
From playlist The Chain Rule and Directional Derivatives, and the Gradient of Functions of Two Variables

Stochastic Approximation-based algorithms, when the Monte (...) - Fort - Workshop 2 - CEB T1 2019
Gersende Fort (CNRS, Univ. Toulouse) / 13.03.2019 Stochastic Approximation-based algorithms, when the Monte Carlo bias does not vanish. Stochastic Approximation algorithms, whose stochastic gradient descent methods with decreasing stepsize are an example, are iterative methods to comput
From playlist 2019 - T1 - The Mathematics of Imaging

Nelly Pustelnik: Optimization -lecture 2
CIRM HYBRID EVENT Recorded during the meeting "Mathematics, Signal Processing and Learning" the January 27, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians o
From playlist Virtual Conference

Emilie Chouzenoux - Deep Unfolding of a Proximal Interior Point Method for Image Restoration
Variational methods have started to be widely applied to ill-posed inverse problems since they have the ability to embed prior knowledge about the solution. However, the level of performance of these methods significantly depends on a set of parameters, which can be estimated through compu
From playlist Journée statistique & informatique pour la science des données à Paris-Saclay 2021

Benjamin Berkels - An introduction to variational image processing - IPAM at UCLA
Recorded 16 September 2022. Benjamin Berkels of RWTH Aachen University presents "An introduction to variational image processing" at IPAM's Computational Microscopy Tutorials. Abstract: This tutorial introduces three fundamental image processing problems, i.e. image denoising, image segmen
From playlist Tutorials: Computational Microscopy 2022

Nelly Pustelnik: Optimization -lecture 3
CIRM HYBRID EVENT Recorded during the meeting "Mathematics, Signal Processing and Learning" the January 27, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians o
From playlist Virtual Conference

Gradient theorem | Lecture 43 | Vector Calculus for Engineers
Derivation of the gradient theorem (or fundamental theorem of calculus for line integrals, or fundamental theorem of line integrals). The gradient theorem shows that the line integral of the gradient of a function is path independent, and only depends on the starting and ending points. J
From playlist Vector Calculus for Engineers

Nelly Pustelnik: Optimization -lecture 4
CIRM HYBRID EVENT Recorded during the meeting "Mathematics, Signal Processing and Learning" the January 27, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians o
From playlist Virtual Conference

Monte Carlo methods and Optimization : Intertwinings (Lecture 4) by Gersende Fort
PROGRAM : ADVANCES IN APPLIED PROBABILITY ORGANIZERS : Vivek Borkar, Sandeep Juneja, Kavita Ramanan, Devavrat Shah and Piyush Srivastava DATE & TIME : 05 August 2019 to 17 August 2019 VENUE : Ramanujan Lecture Hall, ICTS Bangalore Applied probability has seen a revolutionary growth in r
From playlist Advances in Applied Probability 2019

Source separation with proximal and neural network methods - Melchior - Workshop 2 - CEB T3 2018
Peter Melchior (Princeton University) / 26.10.2018 Source separation with proximal and neural network methods ---------------------------------- Vous pouvez nous rejoindre sur les réseaux sociaux pour suivre nos actualités. Facebook : https://www.facebook.com/InstitutHenriPoincare/ Twi
From playlist 2018 - T3 - Analytics, Inference, and Computation in Cosmology

Math: Partial Differential Eqn. - Ch.1: Introduction (11 of 42) What is the Gradient Operator?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is a gradient operator. The gradient operator indicates how much the function is changing when moving a small distance in each of the 3 directions. I will write an example of the gradient
From playlist PARTIAL DIFFERENTIAL EQNS CH1 INTRODUCTION

