
Visual Proof of Pythagoras' Theorem
More resources available at www.misterwootube.com
From playlist Pythagoras’ Theorem

In this video, we present a geometric proof of the Pythagorean theorem. This famous theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Our proof utilizes the prin
From playlist Shorts
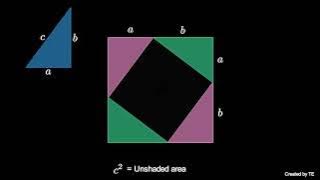
Pythagorean Theorem II (visual proof)
This is a short, animated visual proof of the Pythagorean theorem (the right triangle theorem) using a dissection of a square in two different ways. This theorem states the square of the hypotenuse of a right triangle is equal to the sum of squares of the two other side lengths. #mathshort
From playlist Pythagorean Theorem
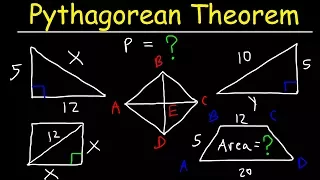
This geometry video tutorial provides a basic introduction into the pythagorean theorem. It explains how to use it to find missing sides and solve for x. In addition, it provides examples of solving word problems using pythagorean theorem for shapes such as right triangles, squares, rhom
From playlist Geometry Video Playlist

Pythagoras: A Simple Geometric Proof
Pythagoras' Theorem is one of the most well-remembered, (in)famous things from our time in maths classes, but all too often the proof of it is skipped out 😥 Because the theorem is such a crucial cornerstone of mathematics - and the theorem can be pretty straight-forward to prove - I've de
From playlist Proofs and Explanations

Geometry: Ch 5 - Proofs in Geometry (6 of 58) Theorems (Pythagorean)
Visit http://ilectureonline.com for more math and science lectures! In this video I will use a non-rigorous method to “proof” the Pythagorean theorem. Next video in this series can be seen at: https://youtu.be/D0fhN7Cfukw
From playlist GEOMETRY 5 - PROOFS IN GEOMETRY

The Pythagorean Theorem I: Two Proofs and a Corollary
Are you interested in math or physics tutoring for you or someone you know? Please check out my website for more details of my registered business, or give me a call or email anytime! https://www.whatthehectogon.com/ +1 (973) 597-8775 sam@whatthehectogon.com In this video lesson, I intr
From playlist Geometry
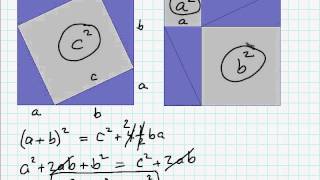
Proofs of the Pythagorean Theorem
The Pythagorean Theorem appears in nearly every branch of mathematics. Here are several proofs drawing from algebra, geometry, and trigonometry.
From playlist Lessons of Interest on Assorted Topics

Converse Pythagorean Theorem & Pythagorean Triples
I explain the Converse Pythagorean Theorem and what Pythagorean Triples are. Find free review test, useful notes and more at http://www.mathplane.com If you'd like to make a donation to support my efforts look for the "Tip the Teacher" button on my channel's homepage www.YouTube.com/Profro
From playlist Geometry

Members’ Colloquium Topic: Thresholds Speaker: Jinyoung Park Affiliation: Stanford University Date: May 16, 2022 Thresholds for increasing properties of random structures are a central concern in probabilistic combinatorics and related areas. In 2006, Kahn and Kalai conjectured that for
From playlist Mathematics

Frédéric Campana: Special manifolds, the core fibration, rational and entire curves
Abstract: For complex projective manifolds X of general type, Lang claimed the equivalence between three fields: birational geometry, complex hyperbolicity, and arithmetic. We extend this equivalence to arbitrary X’s by introducing the (antithetical) class of “Special” manifolds and constr
From playlist Algebraic and Complex Geometry

Hilbert modular eigenvariety at exotic and CM classical points of parallel weight one by Shaunak Deo
PERFECTOID SPACES ORGANIZERS: Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri, and Narasimha Kumar Cheraku DATE & TIME: 09 September 2019 to 20 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France) Eknath
From playlist Perfectoid Spaces 2019

Arithmetic statistics of modular symbols by Morten Risager
PROGRAM : ALGEBRAIC AND ANALYTIC ASPECTS OF AUTOMORPHIC FORMS ORGANIZERS : Anilatmaja Aryasomayajula, Venketasubramanian C G, Jurg Kramer, Dipendra Prasad, Anandavardhanan U. K. and Anna von Pippich DATE & TIME : 25 February 2019 to 07 March 2019 VENUE : Madhava Lecture Hall, ICTS Banga
From playlist Algebraic and Analytic Aspects of Automorphic Forms 2019

Zeta Functions and Cohomology Intro part 1: Standard Conjectures, and Deninger's Conjectures
Here we give a quick and standard introduction to the problems about Zeta functions of varieties over finite fields and then indicate quickly how these are related to a system of problems about the usual Riemann zeta function.
From playlist Riemann Hypothesis

on the Brumer-Stark Conjecture (Lecture 1) by Samit Dasgupta
PROGRAM ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (HYBRID) ORGANIZERS: Ashay Burungale (CalTech/UT Austin, USA), Haruzo Hida (UCLA), Somnath Jha (IIT Kanpur) and Ye Tian (MCM, CAS) DATE: 08 August 2022 to 19 August 2022 VENUE: Ramanujan Lecture Hall and online The program pla
From playlist ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (2022)

Chandrashekhar Khare, Serre's conjecture and computational aspects of the Langlands program
VaNTAGe Seminar, April 5, 2022 License: CC-BY-NC-SA Some relevant links: Edixhoven-Couveignes-de Jong-Merkl-Bosman: https://arxiv.org/abs/math/0605244 Ramanujan's 1916 paper: http://ramanujan.sirinudi.org/Volumes/published/ram18.pdf Delta's home page in the LMFDB: https://www.lmfdb.org/
From playlist Modularity and Serre's conjecture (in memory of Bas Edixhoven)

The threshold for the square of a Hamilton cycleJinyoung Park
Computer Science/Discrete Mathematics Seminar II Topic: The threshold for the square of a Hamilton cycle Speaker: Jinyoung Park Affiliation: Member, School of Mathematics Date: October 20, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Birational Geometry and Orbifold Pairs :Arithmetic and hyperbolic... (Lecture 3) by Frederic Campana
PROGRAM : TOPICS IN BIRATIONAL GEOMETRY ORGANIZERS : Indranil Biswas and Mahan Mj DATE : 27 January 2020 to 31 January 2020 VENUE : Madhava Lecture Hall, ICTS Bangalore Birational geometry is one of the current research trends in fields of Algebraic Geometry and Analytic Geometry. It ca
From playlist Topics In Birational Geometry

Homogeneous spaces, algebraic K-theory and cohomological(...) - Izquierdo - Workshop 2 - CEB T2 2019
Diego Izquierdo (MPIM Bonn) / 24.06.2019 Homogeneous spaces, algebraic K-theory and cohomological dimension of fields. In 1986, Kato and Kuzumaki stated a set of conjectures which aimed at giving a Diophantine characterization of the cohomological dimension of fields in terms of Milnor
From playlist 2019 - T2 - Reinventing rational points

Pythagorean Theorem VII (visual proof)
This is a short, animated visual proof of an extended version of the Pythagorean theorem (the right triangle theorem) that implies the Pythagorean theorem. This theorem states the square of the hypotenuse of a right triangle is equal to the sum of squares of the two other side lengths, and
From playlist Proof Writing