
Proof: What is it, and how does it work?
From playlist The Nature of Proof

How many subsets in a set? (1 of 2: Induction proof)
More resources available at www.misterwootube.com
From playlist The Nature of Proof

In this lecture, Dr Arif Ahmed (University of Cambridge) thinks about the concept of knowledge and the analysis of a particular category of knowledge called ‘propositional knowledge’ (also known as ‘knowledge that’). In particular, we focus on: (i) the distinction between different kinds o
From playlist Philosophy

Geometry: Ch 5 - Proofs in Geometry (5 of 58) How to Proof Proofs
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is and how to proof proofs in geometry. Next video in this series can be seen at: https://youtu.be/xuWliQ6CHpw
From playlist GEOMETRY 5 - PROOFS IN GEOMETRY
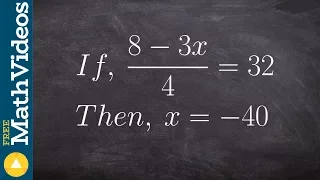
Learning to write an algebraic proof
👉 Learn how to write an algebraic proof. Algebraic proofs are used to help students understand how to write formal proofs where we have a statement and a reason. In the case of an algebraic proof the statement will be the operations used to solve an algebraic equation and the reason will
From playlist Parallel Lines and a Transversal

Proofs by contradiction -- Proofs
This lecture is on Introduction to Higher Mathematics (Proofs). For more see http://calculus123.com.
From playlist Proofs

Ben discusses proof by induction and goes over two examples.
From playlist Basics: Proofs

Efficient Zero Knowledge Proofs - A Modular Approach (Lecture 1) by Yuval Ishai
DISCUSSION MEETING : FOUNDATIONAL ASPECTS OF BLOCKCHAIN TECHNOLOGY ORGANIZERS : Pandu Rangan Chandrasekaran DATE : 15 to 17 January 2020 VENUE : Madhava Lecture Hall, ICTS, Bangalore Blockchain technology is among one of the most influential disruptive technologies of the current decade.
From playlist Foundational Aspects of Blockchain Technology 2020
Zero Knowledge Proofs - Seminar 4 - Non-interactive Zero Knowledge
This seminar series is about the mathematical foundations of cryptography. In this series Eleanor McMurtry is explaining Zero Knowledge Proofs (ZKPs). This seminar continues the development of non-interactive Zero Knowledge protocols, closing in on systems that can be used in practice. Yo
From playlist Metauni

Zero Knowledge Proofs - Seminar 1 - Introduction
This seminar series is about the mathematical foundations of cryptography. In this series Eleanor McMurtry is explaining Zero Knowledge Proofs (ZKPs), a fascinating set of techniques that allow one participant to prove they know something *without revealing the thing*. You can join this s
From playlist Metauni

MPC in the Head With Applications to Blockchain (Lecture 1) by Carmit Hazay
DISCUSSION MEETING : FOUNDATIONAL ASPECTS OF BLOCKCHAIN TECHNOLOGY ORGANIZERS : Pandu Rangan Chandrasekaran DATE : 15 to 17 January 2020 VENUE : Madhava Lecture Hall, ICTS, Bangalore Blockchain technology is among one of the most influential disruptive technologies of the current decade.
From playlist Foundational Aspects of Blockchain Technology 2020

zkSNARKs -- Recent progress and applications to blockchain protocols by Chaya Ganesh
DISCUSSION MEETING : FOUNDATIONAL ASPECTS OF BLOCKCHAIN TECHNOLOGY ORGANIZERS : Pandu Rangan Chandrasekaran DATE : 15 to 17 January 2020 VENUE : Madhava Lecture Hall, ICTS, Bangalore Blockchain technology is among one of the most influential disruptive technologies of the current decade.
From playlist Foundational Aspects of Blockchain Technology 2020

Stanford Seminar - Zero-Knowledge and the Next Digital Revolution
March 6, 2023 Alex Pruden of Aleo

Luca De Feo, Proving knowledge of isogenies, quaternions and signatures
VaNTAGe Seminar, November 15, 2022 License: CC-BY-NC-SA Links to some of the papers and cites mentioned in the talk: Couveignes (2006): https://eprint.iacr.org/2006/291 Fiat-Shamir (1986): https://doi.org/10.1007/3-540-47721-7_12 De Feo-Jao-Plût (2011): https://eprint.iacr.org/2011/506 B
From playlist New developments in isogeny-based cryptography

Zero Knowledge Proofs - Seminar 5 - NP languages have zero knowledge proofs
This seminar series is about the mathematical foundations of cryptography. In this series Eleanor McMurtry is explaining Zero Knowledge Proofs (ZKPs). This seminar covers the 1991 proof by Goldreich-Micali-Widgerson that every NP language has a zero knowledge proof. You can join this semi
From playlist Metauni

Introduction to Proof by Counter Example
This video provides an introduction to the proof method of proof by counter example. mathispower4u.com
From playlist Symbolic Logic and Proofs (Discrete Math)



