
Introduction to the Distributive Property
This video explains the distributive property and provides examples on how to use the distributive property. http://mathispower4u.yolasite.com/
From playlist The Distributive Property and Simplifying Algebraic Expressions

Why does the distributive property Where does it come from
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

How to Simplify an Expression Using Distributive Property - Math Tutorial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials
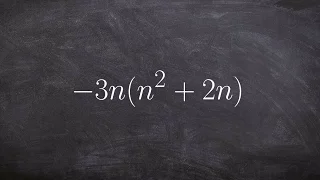
How to Multiply Using the Distributive Property | Simplify by Multiplying
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

How to Learn the Basics of The Distributive Property
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials
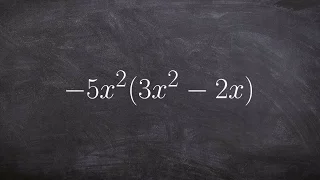
Learn How to Use the Distributive Property to Multiply Polynomials
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

The Distributive Property (L2.4)
This video defines the distributive property and provides several examples of how to multiply using the distributive property. Video content created Jenifer Bohart, William Meacham, Judy Sutor, and Donna Guhse from SCC (CC-BY 4.0)
From playlist The Distributive Property and Simplifying Algebraic Expressions

Welcome to Quantitative Risk Management (QRM). There is so much confusion about tails, that it is time to clarify what we are speaking about. Heavy tails, long tails and fat tails are not the same thing from a statistical and probabilistic point of view. In mathematics we need to be preci
From playlist Quantitative Risk Management

How to Use the Distributive Property to Multiply Binomials - Polynomials
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

Bootstrap and Confidence Intervals
In this video, I explain how to make a confidence interval with bootstrapping. Here, we go over how to make a confidence interval with the true population, how to apply bootstrap to get the confidence interval and finally, I walk you through what happens to the confidence interval as the s
From playlist Introduction to Data Science - Foundations

Plug in Principle - Data Science
In this video, I explain the super important plugin principle! Using this principle, (and some assumptions) allows us to finally talk about topics like population. Here, I explain when to use the principle, what the tradeoffs are, and also go through some examples using it. Enjoy! Link to
From playlist Introduction to Data Science - Foundations

Joscha Prochno: The large deviations approach to high-dimensional convex bodies II
Given any isotropic convex body in high dimension, it is known that its typical random projections will be approximately standard Gaussian. The universality in this central limit perspective restricts the information that can be retrieved from the lower-dimensional projections. In contrast
From playlist Workshop: High dimensional spatial random systems

Joscha Prochno: The large deviations approach to high-dimensional convex bodies, lecture III
Given any isotropic convex body in high dimension, it is known that its typical random projections will be approximately standard Gaussian. The universality in this central limit perspective restricts the information that can be retrieved from the lower-dimensional projections. In contrast
From playlist Workshop: High dimensional spatial random systems

Dmitriy Bilyk: On the interplay between uniform distribution,discrepancy, and energy
VIRTUAL LECTURE Recording during the meeting "Discrepancy Theory and Applications". Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywo
From playlist Analysis and its Applications

Joscha Prochno: The large deviations approach to high-dimensional convex bodies, Lecture I
Given any isotropic convex body in high dimension, it is known that its typical random projections will be approximately standard Gaussian. The universality in this central limit perspective restricts the information that can be retrieved from the lower-dimensional projections. In contrast
From playlist Workshop: High dimensional spatial random systems

The flexibility of caustics and its applications - Daniel Alvarez-Gavela
Workshop on the h-principle and beyond Topic: The flexibility of caustics and its applications Speaker: Daniel Alvarez-Gavela Affiliation: Massachusetts Institute of Technology Date: November 03, 2021 Alvarez-Gavela-2021-11-03 Singularities of smooth maps are flexible: there holds an h
From playlist Mathematics

Limit Theorems in Pseudorandomness - Raghu Meka
Raghu Meka The University of Texas at Austin; Member, School of Mathematics October 3, 2011 For more videos, visit http://video.ias.edu
From playlist Mathematics

Using the Box Method to Multiply a Trinomial by a Trinomial - Math Tutorial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply a Trinomial by a Trinomial

Deep Learning 8: Unsupervised learning and generative models
Shakir Mohamed, Research Scientist, discusses unsupervised learning and generative models as part of the Advanced Deep Learning & Reinforcement Learning Lectures.
From playlist Learning resources