
Prime Numbers and their Mysterious Distribution (Prime Number Theorem)
Primes are the building blocks of math. But just how mysterious are they? Our study of prime numbers dates back to the ancient Greeks who first recognized that certain numbers can't be turned into rectangles, or that they can't be factored into any way. Over the years prime numbers have
From playlist Prime Numbers

Algebra - Ch. 6: Factoring (4 of 55) What is a Prime Number?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is a prime number. A prime number is a positive integer that can only be written as a product of one and itself. Its factors are “1” and itself. To donate: http://www.ilectureonline.com/
From playlist ALGEBRA CH 6 FACTORING
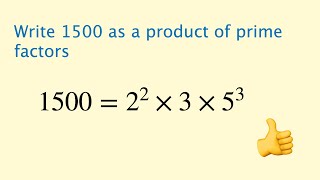
Prime Factoring - GCSE Mathematics Revision (Foundation)
What are prime numbers? Learn how to find the prime factors of a number and write it as a product of prime factors. ❤️ ❤️ ❤️ Support the channel ❤️ ❤️ ❤️ https://www.youtube.com/channel/UCf89Gd0FuNUdWv8FlSS7lqQ/join
From playlist Number

RNT1.4. Ideals and Quotient Rings
Ring Theory: We define ideals in rings as an analogue of normal subgroups in group theory. We give a correspondence between (two-sided) ideals and kernels of homomorphisms using quotient rings. We also state the First Isomorphism Theorem for Rings and give examples.
From playlist Abstract Algebra

Interesting Facts About the Last Digits of Prime Numbers
This video explains some interesting facts about the last digits of prime numbers.
From playlist Mathematics General Interest

An easy intro to prime numbers and composite numbers that MAKES SENSE. What are prime numbers? A prime number is a number that has exactly 2 factors: two and itself. What are composite numbers? A composite number is one which has two or more factors. What is the difference between a p
From playlist Indicies (Exponents) and Primes

Definition of a Ring and Examples of Rings
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Ring and Examples of Rings - Definition of a Ring. - Definition of a commutative ring and a ring with identity. - Examples of Rings include: Z, Q, R, C under regular addition and multiplication The Ring of all n x
From playlist Abstract Algebra

Prealgebra Lecture 4.2: Prime Factorization and Simplification of Fractions
https://www.patreon.com/ProfessorLeonard Prealgebra Lecture 4.2: Prime Factorization and Simplification of Fractions
From playlist Prealgebra (Full Length Videos)

Rings 6 Prime and maximal ideals
This lecture is part of an online course on rings and modules. We discuss prime and maximal ideals of a (commutative) ring, use them to construct the spectrum of a ring, and give a few examples. For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj5
From playlist Rings and modules

Schemes 5: Definition of a scheme
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. We give some historical background, then give the definition of a scheme and some simple examples, and finish by explaining the origin of the word "spectrum".
From playlist Algebraic geometry II: Schemes

Abstract Algebra | The motivation for the definition of an ideal.
Towards the goal of creating a quotient ring, we uncover the defintion of an ideal. http://www.michael-penn.net https://www.researchgate.net/profile/Michael_Penn5 http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Commutative algebra 12: Examples of Spec R
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We give some examples of the spectrum of a ring, including the rings of Gaussian integers, polynomials and power series in 2 v
From playlist Commutative algebra

[Lesson 15 and 1/3] QED Prerequisites Lorentz Transformations: Rod and Ring Paradox
In this lesson we exploit the pure boost transformation matrices to analyse the "Rod and Ring" paradox of special relativity. The key takeaway: two non-colinear boosts are NOT equivalent to any single boost! Please consider supporting this channel on Patreon: https://www.patreon.com/XYL
From playlist QED- Prerequisite Topics

CTNT 2022 - 100 Years of Chebotarev Density (Lecture 1) - by Keith Conrad
This video is part of a mini-course on "100 Years of Chebotarev Density" that was taught during CTNT 2022, the Connecticut Summer School and Conference in Number Theory. More about CTNT: https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2022 - 100 Years of Chebotarev Density (by Keith Conrad)

Visual Group Theory, Lecture 7.3: Ring homomorphisms
Visual Group Theory, Lecture 7.3: Ring homomorphisms A ring homomorphism is a structure preserving map between rings, which means that f(x+y)=f(x)+f(y) and f(xy)=f(x)f(y) both must hold. The kernel is always a two-sided ideal. There are four isomorphism theorems for rings, which are compl
From playlist Visual Group Theory

Commutative algebra 11 (Spectrum of a ring)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we define the spectrum of a ring as the space of prime ideals, and give a few examples. Reading: Lectures 9
From playlist Commutative algebra

Commutative algebra 18 (Functions on Spec R)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we explain how to consider elements of a ring R as functions on the space Spec R, taking values at each point
From playlist Commutative algebra

MegaFavNumbers: Plus One Primes, 154,641,337, and 62,784,382,823
My entry in the #MegaFavNumbers series looks at a particularly striking example of a very specific family of primes -- and how it connects to what digits can be the final digit of primes in different bases.
From playlist MegaFavNumbers

