
Geometry - Ch. 2: Reasoning and Proofs (21 of 46) What is a Postulate?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is a postulate. A postulate, or axium, is a proposition that is not proved or demonstrated but considered to be self evident. It is a “truth” that is accepted. A postulate serves as a sta
From playlist GEOMETRY CH 2 PROOFS & REASONING

Geometry - Ch. 2: Reasoning and Proofs (22 of 46) Postulate 1: Ruler (Numberline)
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain Postulate 1:The Ruler, or Number Line, Postulate – points on a line have corresponding points on a number line such that they can have “x-values” called “coordinates” of the points (x1, x2, x3
From playlist GEOMETRY CH 2 PROOFS & REASONING

More Postulates & Theorems Points, Lines, & Planes
I introduce 5 more postulates relating to points, lines, and planes. These postulates are then used to prove the first three theorems in Geometry. Theorem 1, If 2 lines intersect, then they intersect in exactly one point. Theorem 2, Through a line and a point not in the line there is ex
From playlist Geometry
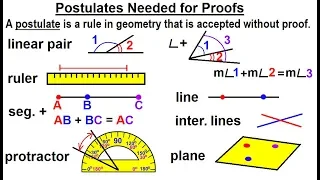
Geometry - Ch. 3: Proofs (5 of 17) Postulates Needed for Proofs
Visit http://ilectureonline.com for more math and science lectures! In this video I will define what is a postulate, and review some of the basic postulates needed for geometry proofs: linear pair, ruler, segment addition, protractor, angle addition, line intersecting lines, and plane. T
From playlist GEOMETRY CH 3 PROOFS

Geometry - Ch. 4: Lines and Angles (2 of 37) Postulates of Parallel and Perpendicular Lines
Visit http://ilectureonline.com for more math and science lectures! In this video I will define and explain postulates of parallel and perpendicular lines. 1) If there is a line and a point not on the line then there is exactly one line through the point PARALLEL to the initial line. 2) I
From playlist GEOMETRY CH 4 LINES AND ANGLES
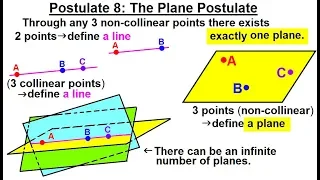
Geometry - Ch. 2: Reasoning and Proofs (29 of 46) Postulate 8: The Plane Postulate
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain Postulate 8: The Plane Postulate – Through any 3 non-collinear points, exists exactly one plane. Next video in this series can be seen at: https://youtu.be/NuiTMuNaUdA
From playlist GEOMETRY CH 2 PROOFS & REASONING

Geometry - Ch. 2: Reasoning and Proofs (28 of 46) Postulate 7: Line Intersect
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain Postulate 7: Line Intersection Postulate – If 2 lines intersect, then their intersection is exactly 1 point. Next video in this series can be seen at: https://youtu.be/2SrWjJ8qSoY
From playlist GEOMETRY CH 2 PROOFS & REASONING

Geometry - Ch. 2: Reasoning and Proofs (34 of 46) Evaluating 3 Postulates
Visit http://ilectureonline.com for more math and science lectures! In this video I will evaluate 3 postulates: Postulate 6: At Least 2 Points Postulate, Postulate 7: Line Intersection Postulate, Postulate 8: The Plane Postulate; given 2 intersecting lines and point F on plane Q. Next vi
From playlist GEOMETRY CH 2 PROOFS & REASONING

AN ELEMENTARY PROOF OF BERTRAND'S POSTULATE! Special #SoMe1
I love when a deep result in mathematics is provable only with elementary techniques, like basic knowledge of combinatorics and arithmetic. In this video I will present the queen of this proofs, namely the Erdős' proof of the Bertrand's postulate, which states that it is always possible to
From playlist Summer of Math Exposition Youtube Videos

Singular Hodge theory of matroids - Jacob Matherne
Joint IAS/Princeton University Algebraic Geometry Seminar Topic: Singular Hodge theory of matroids Speaker: Jacob Matherne Affiliation: Member, School of Mathematics Date: March 25, 2019 For more video please visit http://video.ias.edu
From playlist Joint IAS/PU Algebraic Geometry

David Meyer (1/30/18): Some algebraic stability theorems for generalized persistence modules
From an algebraic point of view, generalized persistence modules can be interpreted as finitely-generated modules for a poset algebra. We prove an algebraic analogue of the isometry theorem of Bauer and Lesnick for a large class of posets. This theorem shows that for such posets, the int
From playlist AATRN 2018

Clark Barwick - 2/3 Exodromy for ℓ-adic Sheaves
In joint work with Saul Glasman and Peter Haine, we proved that the derived ∞-category of constructible ℓ-adic sheaves ’is’ the ∞-category of continuous functors from an explicitly defined 1-category to the ∞-category of perfect complexes over ℚℓ. In this series of talks, I want to offer s
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Ulysses Alvarez - The Up Topology on the Grassmann Poset
38th Annual Geometric Topology Workshop (Online), June 15-17, 2021 Ulysses Alvarez, Binghamton University Title: The Up Topology on the Grassmann Poset Abstract: For a discrete poset X, McCord proved that there exists a weak homotopy equivalence from the order complex |X| to where X has
From playlist 38th Annual Geometric Topology Workshop (Online), June 15-17, 2021

Patrick Ingram, The critical height of an endomorphism of projective space
VaNTAGe seminar on June 9, 2020. License: CC-BY-NC-SA. Closed captions provided by Matt Olechnowicz
From playlist Arithmetic dynamics

Pavel Etingof - "D-modules on Poisson varieties and Poisson traces"
Pavel Etingof delivers a research talk on "D-modules on Poisson varieties and Poisson traces" at the Worldwide Center of Mathematics
From playlist Center of Math Research: the Worldwide Lecture Seminar Series

Christian Gaetz: "Antichains and intervals in the weak order"
Asymptotic Algebraic Combinatorics 2020 "Antichains and intervals in the weak order" Christian Gaetz - Massachusetts Institute of Technology Abstract: The weak order is the partial order on the symmetric group S_n (or other Coxeter group) whose cover relations correspond to simple transp
From playlist Asymptotic Algebraic Combinatorics 2020

Becca Winarski: Characterizing Thurston maps by lifting trees
HYBRID EVENT Recorded during the meeting "Advancing Bridges in Complex Dynamics" the September 23, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Luca Récanzone Find this video and other talks given by worldwide mathematicians on CIRM's Audi
From playlist Topology

Assaf Rinot : Distributive Aronszajn trees
Abstract: It is well-known that the statement "all ℵ1-Aronszajn trees are special'' is consistent with ZFC (Baumgartner, Malitz, and Reinhardt), and even with ZFC+GCH (Jensen). In contrast, Ben-David and Shelah proved that, assuming GCH, for every singular cardinal λ: if there exists a λ+-
From playlist Logic and Foundations

Calculus 5.3 The Fundamental Theorem of Calculus
My notes are available at http://asherbroberts.com/ (so you can write along with me). Calculus: Early Transcendentals 8th Edition by James Stewart
From playlist Calculus

Singular Hodge Theory for Combinatorial Geometries by Jacob Matherne
PROGRAM COMBINATORIAL ALGEBRAIC GEOMETRY: TROPICAL AND REAL (HYBRID) ORGANIZERS: Arvind Ayyer (IISc, India), Madhusudan Manjunath (IITB, India) and Pranav Pandit (ICTS-TIFR, India) DATE & TIME: 27 June 2022 to 08 July 2022 VENUE: Madhava Lecture Hall and Online Algebraic geometry is t
From playlist Combinatorial Algebraic Geometry: Tropical and Real (HYBRID)