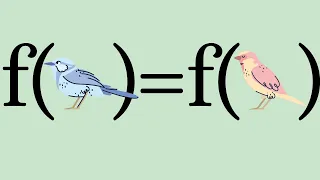Combinatorics | Mathematical principles | Theorems in discrete mathematics | Ramsey theory
Pigeonhole principle
In mathematics, the pigeonhole principle states that if n items are put into m containers, with n > m, then at least one container must contain more than one item. For example, if one has three gloves (and none is ambidextrous/reversible), then there must be at least two right-handed gloves, or at least two left-handed gloves, because there are three objects, but only two categories of handedness to put them into. This seemingly obvious statement, a type of counting argument, can be used to demonstrate possibly unexpected results. For example, given that the population of London is greater than the maximum number of hairs that can be present on a human's head, then the pigeonhole principle requires that there must be at least two people in London who have the same number of hairs on their heads. Although the pigeonhole principle appears as early as 1624 in a book attributed to Jean Leurechon, it is commonly called Dirichlet's box principle or Dirichlet's drawer principle after an 1834 treatment of the principle by Peter Gustav Lejeune Dirichlet under the name Schubfachprinzip ("drawer principle" or "shelf principle"). The principle has several generalizations and can be stated in various ways. In a more quantified version: for natural numbers k and m, if n = km + 1 objects are distributed among m sets, then the pigeonhole principle asserts that at least one of the sets will contain at least k + 1 objects. For arbitrary n and m, this generalizes to where and denote the floor and ceiling functions, respectively. Though the most straightforward application is to finite sets (such as pigeons and boxes), it is also used with infinite sets that cannot be put into one-to-one correspondence. To do so requires the formal statement of the pigeonhole principle, which is "there does not exist an injective function whose codomain is smaller than its domain". Advanced mathematical proofs like Siegel's lemma build upon this more general concept. (Wikipedia).