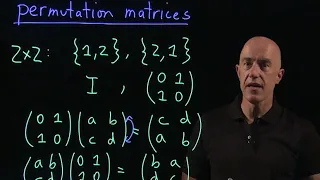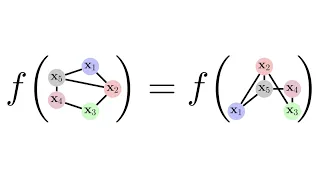Sparse matrices | Permutations | Matrices
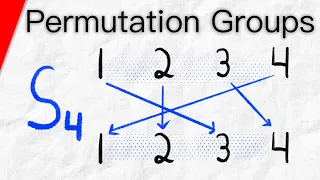
Permutation matrix
In mathematics, particularly in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry of 1 in each row and each column and 0s elsewhere. Each such matrix, say P, represents a permutation of m elements and, when used to multiply another matrix, say A, results in permuting the rows (when pre-multiplying, to form PA) or columns (when post-multiplying, to form AP) of the matrix A. (Wikipedia).