
Complex Numbers as Points (1 of 4: Geometric Meaning of Addition)
More resources available at www.misterwootube.com
From playlist Complex Numbers

Perfect Numbers and Euler's Theorem
A perfect number is a number that equals the sum of its proper factors. How can we find them?
From playlist Math Play

What are complex numbers? | Essence of complex analysis #2
A complete guide to the basics of complex numbers. Feel free to pause and catch a breath if you feel like it - it's meant to be a crash course! Complex numbers are useful in basically all sorts of applications, because even in the real world, making things complex sometimes, oxymoronicall
From playlist Essence of complex analysis

Completeness and Orthogonality
A discussion of the properties of Completeness and Orthogonality of special functions, such as Legendre Polynomials and Bessel functions.
From playlist Mathematical Physics II Uploads

Introduction to Complex Numbers (Free Ebook)
http://bookboon.com/en/introduction-to-complex-numbers-ebook This free ebook makes learning "complex" numbers easy through an interactive, fun and personalized approach. Features include: live YouTube video streams and closed captions that translate to 90 languages! Complex numbers "break
From playlist Intro to Complex Numbers

One of the oldest unsolved math problems is studying odd perfect numbers. Have fun learning the many math approaches to this problem.
From playlist Summer of Math Exposition 2 videos

Alexander Efimov - Relative derived categories and matrix factorizations
Alexander EFIMOV (Steklov Mathematical Institute, RAS, Moscow, Russia)
From playlist Algèbre, Géométrie et Physique : une conférence en l'honneur

Geometric noncommutative schemes, their gluing and finite dimensional algebras - Dmitry Orlov
Dmitry Orlov March 10, 2015 Workshop on Chow groups, motives and derived categories More videos on http://video.ias.edu
From playlist Mathematics

Perfect complexes, Lefschetz trace formula with torsion coefficients, intro to the main lemma
From playlist Étale cohomology and the Weil conjectures

Introduction to Smith theory - Tony Feng
Geometric and Modular Representation Theory Seminar Topic: Introduction to Smith theory Speaker: Tony Feng Affiliation: Member, School of Mathematics Date: January 13, 2021 For more video please visit http://video.ias.edu
From playlist Seminar on Geometric and Modular Representation Theory

Charles Weibel: K-theory of algebraic varieties (Lecture 2)
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Charles Weibel: K theory of algebraic varieties Abstract: Lecture 1 will present definitions for the Waldhausen K-theory of rings, varieties, additive and exact categories, and dg c
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Special Values of Zeta Functions (Lecture 1) by Matthias Flach
PROGRAM ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (HYBRID) ORGANIZERS: Ashay Burungale (CalTech/UT Austin, USA), Haruzo Hida (UCLA), Somnath Jha (IIT Kanpur) and Ye Tian (MCM, CAS) DATE: 08 August 2022 to 19 August 2022 VENUE: Ramanujan Lecture Hall and online The program pla
From playlist ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (2022)

Peter SCHOLZE (oct 2011) - 3/6 Perfectoid Spaces and the Weight-Monodromy Conjecture
We will introduce the notion of perfectoid spaces. The theory can be seen as a kind of rigid geometry of infinite type, and the most important feature is that the theories over (deeply ramified extensions of) Q_p and over F_p((t)) are equivalent, generalizing to the relative situation a th
From playlist Peter SCHOLZE (oct 2011) - Perfectoid Spaces and the Weight-Monodromy Conjecture
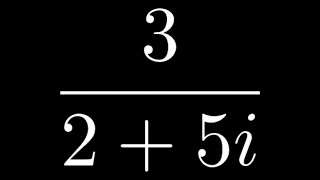
Dividing Complex Numbers Example
Dividing Complex Numbers Example Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys
From playlist Complex Numbers

Abundant, Deficient, and Perfect Numbers ← number theory ← axioms
Integers vary wildly in how "divisible" they are. One way to measure divisibility is to add all the divisors. This leads to 3 categories of whole numbers: abundant, deficient, and perfect numbers. We show there are an infinite number of abundant and deficient numbers, and then talk abou
From playlist Number Theory




