
Use the Remainder Theorem to Determine if a Binomial is a Factor of a Polynomial
This video explains how to use the remainder theorem to determine if a binomial is a factor of a given polynomial. http://mathispower4u.com
From playlist Finding the Zeros of Polynomial Functions

What is the remainder theorem for polynomials
👉 Learn about the remainder theorem and the factor theorem. The remainder theorem states that when a polynomial is divided by a linear expression of the form (x - k), the remainder from the division is equivalent to f(k). Similarly, when a polynomial is divided by a linear expression of th
From playlist Remainder and Factor Theorem | Learn About

Using the remainder theorem and checking your answer with synthetic division
👉 Learn about and how to apply the remainder and factor theorem. The remainder theorem states that f(a) is the remainder when the polynomial f(x) is divided by x - a. Thus, given a polynomial, f(x), which is to be divided by a linear binomial of form x - a, the remainder of the division is
From playlist Remainder and Factor Theorem

Introduction to additive combinatorics lecture 10.8 --- A weak form of Freiman's theorem
In this short video I explain how the proof of Freiman's theorem for subsets of Z differs from the proof given earlier for subsets of F_p^N. The answer is not very much: the main differences are due to the fact that cyclic groups of prime order do not have lots of subgroups, so one has to
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)
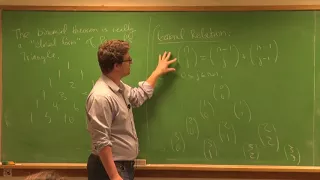
Fundamentals of Mathematics - Lecture 17: Binomial Theorem (and Orderings)
course page: https://www.uvm.edu/~tdupuy/logic/Math52-Fall2017.html worksheets - DZB, Emory videography - Eric Melton, UVM
From playlist Fundamentals of Mathematics
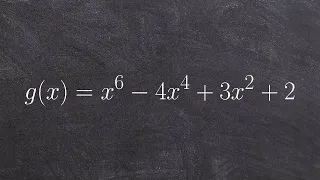
Using the remainder theorem to confirm if you have a zero or not
👉 Learn about and how to apply the remainder and factor theorem. The remainder theorem states that f(a) is the remainder when the polynomial f(x) is divided by x - a. Thus, given a polynomial, f(x), which is to be divided by a linear binomial of form x - a, the remainder of the division is
From playlist Remainder and Factor Theorem

Lecture 2: Multiplying and Factoring Matrices
MIT 18.065 Matrix Methods in Data Analysis, Signal Processing, and Machine Learning, Spring 2018 Instructor: Gilbert Strang View the complete course: https://ocw.mit.edu/18-065S18 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP63oMNUHXqIUcrkS2PivhN3k Multiplying and fa
From playlist MIT 18.065 Matrix Methods in Data Analysis, Signal Processing, and Machine Learning, Spring 2018

👉 Learn about the remainder theorem and the factor theorem. The remainder theorem states that when a polynomial is divided by a linear expression of the form (x - k), the remainder from the division is equivalent to f(k). Similarly, when a polynomial is divided by a linear expression of th
From playlist Remainder and Factor Theorem | Learn About
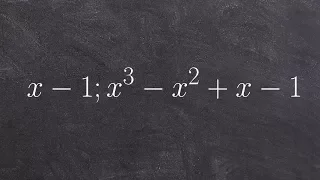
How to use the remainder theorem for polynomials
👉 Learn about and how to apply the remainder and factor theorem. The remainder theorem states that f(a) is the remainder when the polynomial f(x) is divided by x - a. Thus, given a polynomial, f(x), which is to be divided by a linear binomial of form x - a, the remainder of the division is
From playlist Remainder and Factor Theorem

Maxwell’s Demon Goes Optical! by Swapan Chattopadhyay
DISTINGUISHED LECTURES MAXWELL’S DEMON GOES OPTICAL! SPEAKER: Swapan Chattopadhyay (FNAL, USA & IISc, India) DATE: 15 November 2022, 17:30 to 18:30 VENUE: Chandrasekhar Auditorium Abstract: Stochastic phase space cooling using microwave techniques in the GHz frequency range have been
From playlist DISTINGUISHED LECTURES

Gregory Miermont - Un panorama des limites d'échelles de cartes aléatoires
UMPA, ENS Lyon, Prix Jaffé 2016 Réalisation technique : Antoine Orlandi (GRICAD) | Tous droits réservés
From playlist Des mathématiciens primés par l'Académie des Sciences 2017

Jeff Calder: "An intro to concentration of measure with applications to graph-based l... (Part 1/2)"
Watch part 2/2 here: https://youtu.be/O20JHvI-MqE High Dimensional Hamilton-Jacobi PDEs Tutorials 2020 "An introduction to concentration of measure with applications to graph-based learning (Part 1/2)" Jeff Calder, University of Minnesota - Twin Cities Abstract: We will give a gentle in
From playlist High Dimensional Hamilton-Jacobi PDEs 2020
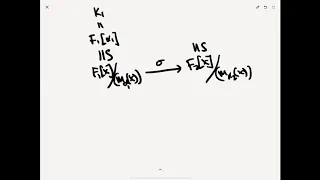
Field Theory - the Extension Lemma - Lecture 14
--Let \sigma: F_1 \to F_2 be an isomorphism of fields. --Let f_1(x) \in F_1[x] and let f_2(x) be the image in f_1(x) under the natural isomorphism F_1[x] \to F_2[x]. --Let L_1 is the splitting field of f_1(x) and L_2 the splitting field of f_2(x). Lemma: The isomorphism \sigma extends t
From playlist Field Theory

Stephanos Venakides: Rigorous semiclassical asymptotics for integrable systems
The title of the lecture is shortened to comply with Youtubes' title policy. The original title of this lecture is "Rigorous semiclassical asymptotics for integrable systems:The KdV and focusing NLS cases". Programme for the Abel Lectures 2005: 1. "Abstract Phragmen-Lindelöf theorem & Sa
From playlist Abel Lectures

How to determine if a factor is a factor of a polynomial using factor theorem
👉 Learn about and how to apply the remainder and factor theorem. The remainder theorem states that f(a) is the remainder when the polynomial f(x) is divided by x - a. Thus, given a polynomial, f(x), which is to be divided by a linear binomial of form x - a, the remainder of the division is
From playlist Remainder and Factor Theorem

Spectra of metric graphs and crystalline measures - Peter Sarnak
Members' Seminar Topic: Spectra of metric graphs and crystalline measures Speaker: Peter Sarnak Affiliation: Professor, School of Mathematics Date: February 10, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Nicolas Curien: Random maps and hyperbolic surfaces
CONFERENCE Recorded during the meeting " Structures on Surfaces " the May 02, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathema
From playlist Probability and Statistics

👉 Learn about and how to apply the remainder and factor theorem. The remainder theorem states that f(a) is the remainder when the polynomial f(x) is divided by x - a. Thus, given a polynomial, f(x), which is to be divided by a linear binomial of form x - a, the remainder of the division is
From playlist Remainder and Factor Theorem

Dawid Kielak: Computing fibring of 3-manifoldsand free-by-cyclic groups
Abstract : We will discuss an analogy between the structure of fibrings of 3-manifolds and free-by-cyclic groups; we will focus on effective computability. This is joint work with Giles Gardam. Codes MSC : 20F65, 57K31, 20E36 Keywords : free-by-cyclic groups, fibering, Thurston norm, Thur
From playlist Virtual Conference

Determine if you have a factor of a polynomial using the factor theorem
👉 Learn about and how to apply the remainder and factor theorem. The remainder theorem states that f(a) is the remainder when the polynomial f(x) is divided by x - a. Thus, given a polynomial, f(x), which is to be divided by a linear binomial of form x - a, the remainder of the division is
From playlist Remainder and Factor Theorem